Πώς η ναυσιπλοΐα συνδέεται με την Αστρονομία; – Μέρος Β

Στο πρώτο μέρος είδαμε πώς μπορούμε να χρησιμοποιήσουμε τα ουράνια σώματα για να υπολογίσουμε το γεωγραφικό πλάτος στο οποίο βρισκόμαστε. Η μισή δουλειά έχει γίνει. Τι γίνεται όμως με το γεωγραφικό μήκος;

Φανταστείτε τώρα ότι μεταφέρεστε στο – όχι και τόσο μακρινό – παρελθόν, και συγκεκριμένα στο Λονδίνο, στις αρχές Ιουλίου του 1714. Μαθαίνετε εκεί έκπληκτοι ότι η κυβέρνηση προσφέρει 10 χιλιάδες λίρες (οι οποίες μεταφράζονται σε πολύ περισσότερα χρήματα σε σημερινή αξία) σε όποιον λύσει το πρόβλημα του προσδιορισμού του γεωγραφικού μήκους (Longitude Act) με ακρίβεια μιας μοίρας. Ας ξεπεράσουμε το πρόβλημα της μη ύπαρξης κινητών (και άρα εφαρμογών πλοήγησης) την εποχή εκείνη και ας συνεχίσουμε την ιστορική μας αναδρομή στη ναυσιπλοΐα και τη σχέση της με την αστρονομία!

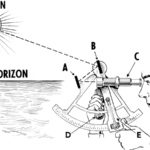
Όπως ίσως θυμάστε, για την εύρεση του γεωγραφικού πλάτους αναφερθήκαμε στους παράλληλους της Γης. Ας χρησιμοποιήσουμε τώρα τους μεσημβρινούς και συγκεκριμένα ας εστιάσουμε στον διάσημο μεσημβρινό του Greenwich, που διέρχεται από το ομώνυμο αστεροσκοπείο. Σε μια ημέρα, η Γη θα έχει εκτελέσει μια πλήρη περιστροφή, δηλαδή μια στροφή γύρω από τον άξονά της κατά 360 μοίρες. Διαιρώντας επομένως 360 μοίρες / 24ώρες,  βρίσκουμε ότι μια γωνιακή απόσταση 15 μοιρών μεταξύ δύο μεσημβρινών αντιστοιχεί σε μια ώρα ή με άλλα λόγια ότι η Γη περιστρέφεται 1 μοίρα κάθε 4 λεπτά.

Επομένως, το πρόβλημα λύθηκε. Βλέποντας την ώρα που ένα αστέρι (π.χ. ο Ήλιος) μεσουρανεί στη θέση που βρισκόμαστε και γνωρίζοντας την ώρα που αυτό συμβαίνει στο σημείο εκκίνησης, βρίσκουμε σε πόσες μοίρες αντιστοιχεί η μετατόπισή μας ανατολικά ή δυτικά¹. Εύκολο.

Στη θεωρία, ναι. Δυστυχώς όμως αυτή η απλή μέθοδος απαιτεί μεγάλη ακρίβεια στη μέτρηση του χρόνου, αρκετή για να σας στερήσει το βραβείο! Την εποχή εκείνη, η μέτρηση του χρόνου πρακτικά κάθε άλλο παρά εύκολη ήταν. Τα ρολόγια ήταν ακριβά και “έχαναν” πολύτιμα δευτερόλεπτα ή και ακόμα λεπτά. Σχετικά πιο ακριβή (και ακριβά!) ήταν τα γνωστά ρολόγια με εκκρεμές. Ακόμα και αυτά όμως δεν έλυναν το πρόβλημα, καθώς ακόμα και σε μια γαλήνια μέρα, οι μικρές κινήσεις του πλοίου, διαφορές στη θερμοκρασία και στην υγρασία, επιδρούσαν στη μέτρηση του χρόνου. Περιττό να αναφέρουμε ότι ένα εκκρεμές σε ένα πλοίο που ταξιδεύει σε φουρτουνιασμένη θάλασσα, κάθε άλλο παρά ακριβές ήταν!

Τη λύση έδωσε ο John Harrison με την κατασκευή ειδικών ρολογιών, τα οποία ονομάστηκαν H1, H2, H3, H4 (Εικόνα 1). Τα ρολόγια αυτά (ή μετρητές χρόνου – timekeepers όπως τα ονόμαζε ο ίδιος), είχαν ειδική σχεδίαση ώστε να μειώνονται τα σφάλματα που αναφέρθηκαν παραπάνω. 

Ιδιαίτερα αξιομνημόνευτο σε αυτή την ιστορία είναι ότι ο Harrison ήταν μαραγκός στο επάγγελμα και αυτοδίδακτος ωρολογοποιός! Το 1736 προγραμματίστηκε η πρώτη δοκιμή του H1, κατά την οποία επιβεβαιώθηκε η ακρίβειά του. Μάλιστα, κατά τη διάρκεια του ταξιδιού, ο Harrison κατάφερε να προσδιορίσει ένα λάθος των αξιωματικών για τη θέση του πλοίου. Ο δρόμος για μια ασφαλέστερη πλοήγηση στις θάλασσες, είχε πλέον ανοίξει. 

^{1 Μια εναλλακτική μέθοδος, η οποία όμως απαιτούσε ακριβέστατους υπολογισμούς, ήταν η μέθοδος μέτρησης της σεληνιακής απόστασης, δηλαδή της απόστασης μεταξύ της Σελήνης και κάπου άλλου ουράνιου σώματος, π.χ. ενός αστέρα. Περισσότερες πληροφορίες για τη μέθοδο: https://www.rmg.co.uk/stories/topics/longitude-found-nevil-maskelyne-lunar-method} 

Επιπλέον υλικό:

1. https://www.rmg.co.uk/stories/topics/harrisons-clocks-longitude-problem