Πώς η ναυσιπλοΐα συνδέεται με την Αστρονομία; – Μέρος Γ

Σε προηγούμενα άρθρα μας (μέρος α, β) είδαμε πώς μπορούμε να βρούμε το γεωγραφικό μας μήκος και πλάτος, χρησιμοποιώντας ένα ακριβές ρολόι και έναν εξάντα, ενώ αναφερθήκαμε και στις εντυπωσιακές για την εποχή εφευρέσεις του J. Harrison¹. Κλείνοντας αυτή τη σειρά άρθρων για τη σύνδεση ναυσιπλοΐας και αστρονομίας, θα περιγράψουμε τη μέθοδο της σεληνιακής απόστασης (lunar distance method) και θα φέρουμε στο προσκήνιο² τον Nevil Maskelyne, Πέμπτο Βασιλικό Αστρονόμο (5^th Astronomer Royal) στο αστεροσκοπείο του Greenwich, ο οποίος την προώθησε.

Πριν όμως εξηγήσουμε πώς ακριβώς δουλεύει η μέθοδος αυτή, αξίζει να εξηγήσουμε πρώτα τη ναυσιπλοΐα εξ αναμετρήσεως (dead reckoning), η οποία χρησιμοποιούταν συστηματικά εκείνη την εποχή. Ένας σχετικά εύκολος τρόπος είναι ο εξής: ας υποθέσουμε ότι ξεκινάμε από το σημείο Α με μόνο εφόδιο μια πυξίδα και ένα ρολόι. Περπατάμε για 1 ώρα με κατεύθυνση προς Βορρά (Β), στη συνέχεια για άλλη μια ώρα με κατεύθυνση βορειοανατολικά (ΒΑ).

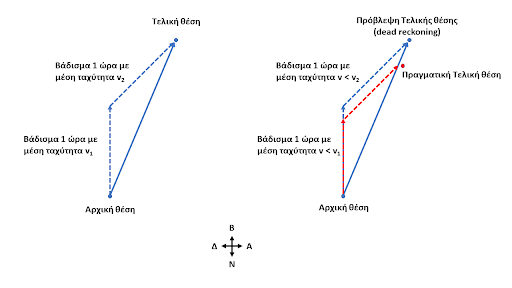
Ποια είναι η τελική μας θέση ως προς το σημείο Α; Η απάντηση μπορεί να δοθεί μόνο προσεγγιστικά, υποθέτοντας ότι περπατήσαμε με μια σχετικά σταθερή μέση ταχύτητα σε όλη τη διάρκεια του ταξιδιού. Εφόσον ξέρουμε την ώρα και τη διεύθυνση της κίνησης, μπορούμε τότε να βρούμε την τελική μας θέση (Εικόνα 1, αριστερά). Αυτό είναι μια απλουστευμένη εκδοχή του dead reckoning. Φυσικά, αυτό προϋποθέτει ότι γνωρίζουμε με πολύ καλή ακρίβεια τη μέση ταχύτητα, το χρόνο και τη διεύθυνση της κίνησης. Ακόμα και μια μικρή απόκλιση σε αυτές τις παραμέτρους, ενδεχομένως να οδηγήσει σε μεγάλο σφάλμα (Εικόνα 1, δεξιά). Φανταστείτε τώρα ακόμα πιο πολύπλοκες διαδρομές, με λιγότερο ακριβή όργανα!

Όπως ίσως ήδη καταλάβατε, τα πράγματα στη θάλασσα είναι αρκετά πιο δύσκολα! Πέραν της αβεβαιότητας στη μέση ταχύτητα και τη διεύθυνση κίνησης (και της ώρας, όπως θα συμπλήρωνε ο J. Harrison!), θα πρέπει κανείς να υπολογίσει την επίδραση του ανέμου, των κυμάτων και των ρευμάτων στο πλοίο. Βλέπουμε λοιπόν ότι το dead reckoning είναι αρκετά δύσκολο να δώσει ακριβή αποτελέσματα σε τέτοιες περίπλοκες συνθήκες.

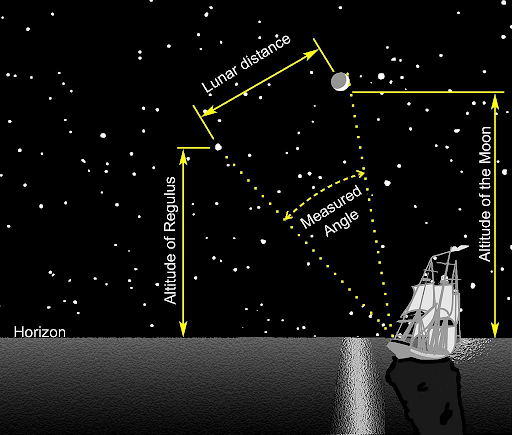
Μια εναλλακτική λύση για την εύρεση του γεωγραφικού μήκους ήταν η μέθοδος της σεληνιακής απόστασης, η οποία βασίζεται στη γωνιακή απόσταση μεταξύ της Σελήνης και ενός άλλου ουράνιου σώματος, για παράδειγμα ενός γνωστού, φωτεινού άστρου (Εικόνα 2). Έχοντας μετρήσει τη γωνιακή απόσταση (π.χ. με έναν εξάντα), ο πλοηγός συμβουλευόταν έναν πίνακα με τις σεληνιακές αποστάσεις, καθώς και τις ώρες που αυτές παρατηρούνται στο Greenwich, κάνοντας τις κατάλληλες διορθώσεις³. Γνωρίζοντας επομένως τη διαφορά ώρας, είναι εύκολο να βρεθεί το γεωγραφικό πλάτος, όπως είδαμε σε προηγούμενο άρθρο.

Σημαντική συνεισφορά στην ανάπτυξη της ιδέας αυτής είχαν οι Tobias Mayer (αστρονόμος στο Ανόβερο) και ο James Bradley (3^rd Astronomer Royal). Οι λεπτομερείς παρατηρήσεις του Mayer είχαν αρχίσει να κερδίζουν έδαφος στα μέσα του 18^ου αιώνα. O Bradley ζήτησε από τον τεχνίτη John Bird να φτιάξει ένα όργανο βασισμένο σε σχέδια του Mayer, το οποίο έμελλε να είναι ο πρώτος ακριβής ναυτικός εξάντας. Μετά από αρκετές βελτιώσεις, ο Bradley θεώρησε ότι το όργανο αυτό μαζί με τις παρατηρήσεις του Mayer θα μπορούσαν να πετύχουν το στόχο εύρεσης του γεωγραφικού μήκους με απόκλιση 1^ο.

Η μέθοδος δοκιμάστηκε σε ένα ταξίδι στο νησί της Αγίας Ελένης (ο τελευταίος τόπος εξορίας του Ναπολέοντα) το 1761. Ο Maskelyne (που είχε αποφοιτήσει εκείνη την περίοδο από το Cambridge και δούλευε με τον Bradley) κατόρθωσε να υπολογίσει το γεωγραφικό μήκος με σφάλμα 1.5^ο μόνο. Η τιμή αυτή αποτελούσε σημαντική βελτίωση σε σχέση με τα σφάλματα του dead reckoning που έφταναν και τις 10^ο! Κατά την επιστροφή του, ο Maskelyne υποστήριξε ότι το πρόβλημα εύρεσης του γεωγραφικού μήκους σε ένα ναυτικό ταξίδι ήταν πλέον εύκολο να λυθεί, αν κάποιος είχε αρκετό χρόνο να κάνει τους απαραίτητους υπολογισμούς. Ωστόσο οι υπολογισμοί αυτοί ήταν τελικά αρκετά δύσκολοι και χρονοβόροι⁴. Η μέθοδος θα γινόταν πιο εύχρηστη αν οι μελλοντικές θέσεις της Σελήνης είχαν συγκεντρωθεί σε πίνακες, μια ιδέα που ο Maskelyne πήρε από το γαλλικό Almanac Connaissance des temps.

Ο Maskelyne οργάνωσε τη συγγραφή των Ναυτικών Αλμανάκ και των Αστρονομικών Εφημερίδων, καθώς και την επικαιροποίησή τους (με πολλούς βοηθούς του να αναλαμβάνουν αυτό τον αρκετά άχαρο ρόλο). Η ιστορία τελειώνει (;) κάπου εδώ⁵. Ωστόσο, για αρκετό διάστημα, όλες οι μέθοδοι που παρουσιάσαμε θα χρησιμοποιούνταν παράλληλα, μέχρι οι πλοηγοί να εκπαιδευτούν κατάλληλα και τα όργανα να τελειοποιηθούν.

¹ Αρχικά, υπήρχε δυσπιστία ως προς την ακρίβεια των ρολογιών του Harrison, ενώ στη συνέχεια η αρμόδια επιτροπή ανησυχούσε ότι το κόστος κατασκευής τους θα ήταν απαγορευτικό ώστε να χρησιμοποιηθούν ευρέως.

² Η  ιστορία του «αυτοδίδακτου εφευρέτη» Harrison συχνά επισκιάζει τη συμβολή του Maskelyne.

³ Στο σημείο αυτό αναφερόμαστε στην παράλλαξη, τη διαφορά στη φαινόμενη θέση ενός αντικειμένου όταν αυτό παρατηρείται από δύο διαφορετικές θέσεις.

⁴ Ο Νεύτωνας σχολίασε σε επιτροπή της Βουλής των Κοινοτήτων το 1714 ότι και οι τέσσερις μέθοδοι που είχαν προταθεί για την εύρεση του γεωγραφικού μήκους ήταν προβληματικές, για διαφορετικούς όμως λόγους. Αυτές ήταν η χρήση ρολογιών, μέτρηση της σεληνιακή απόσταση, μελέτη των εκλείψεων των φεγγαριών του Δία καθώς και… η χρήση όλμων από αγκυροβολημένα πλοία!

⁵ Μια ιστορία που ξεκίνησε το 1707 με την απώλεια τεσσάρων πολεμικών πλοίων του Βασιλικού Βρετανικού Ναυτικού, την ψήφιση του Longitude Act το 1714 και συνεχίστηκε με τις δοκιμές των Maskelyne και Harrison, αλλά και τη συνεισφορά πολλών άλλων αστρονόμων!