Υπάρχουν επιπλέον διαστάσεις;

Αυτή είναι μια ερώτηση που απασχολεί την επιστήμη εδώ και δεκαετίες. Πριν όμως αναρωτηθούμε για το αν υπάρχουν επιπλέον διαστάσεις, ας κατανοήσουμε σε πόσες διαστάσεις ζούμε σήμερα.

Εδώ και 100 περίπου χρόνια, η επιστημονική κοινότητα έχει αποδεχθεί τον αριθμό 4 ως το πλήθος των διαστάσεων: τρεις χωρικές και μια διάσταση χρόνου. Από τη στιγμή που αντιλαμβανόμαστε τον κόσμο γύρω μας, οι αισθήσεις μας αναγνωρίζουν τις τρεις χωρικές διαστάσεις ως κάτι το μοναδικό και παράλληλα τόσο οικείο. Χρειάζεται να καταβάλλουμε αρκετή προσπάθεια ώστε να φανταστούμε (αν τα καταφέρουμε) πως θα αντιλαμβανόμαστε τον κόσμο γύρω μας, αν για παράδειγμα ήμασταν όντα δύο διαστάσεων.

Η αλλαγή του χρόνου είναι επίσης αντιληπτή από τις αισθήσεις μας. Είναι όμως αυτό αρκετό ώστε να χαρακτηριστεί ο χρόνος ως διάσταση; Αυτός ο περιορισμός των αισθήσεων, εξαφανίζεται με τη χρήση των μαθηματικών. Εκεί, μια επιπλέον ή μια λιγότερη διάσταση είναι απλά μια αλλαγή τους πλήθους των μεταβλητών. Στη Νευτώνεια Φυσική, τα γεγονότα που συμβαίνουν γύρω μας εκτυλίσσονται σε έναν απόλυτο χώρο τριών διαστάσεων, και η εξέλιξη τους δίνεται ως συνάρτηση του απόλυτου χρόνου, η οποία θεωρείται μια εξωτερική παράμετρος και όχι διάσταση.

Αυτή η θεώρηση μπόρεσε να εξηγήσει πληθώρα φυσικών φαινομένων, πλην όμως αρκετών φαινομένων που σχετίζονται με τη φύση του φωτός και του ηλεκτρομαγνητισμού. Η αλλαγή στη θεώρηση του χρόνου έγινε από τον Einstein στην περίφημη εργασία του (μετάφραση: On the electrodynamics of moving bodies, June 30 1905 -Περί της ηλεκτροδυναμικής των κινούμενων σωμάτων-), στην οποία όμως ο χρόνος δεν αντιμετωπίζεται ως διάσταση. Στις 21 Σεπτεμβρίου 1908 ο Herman Minkowski εισήγαγε το χρόνο ως διάσταση σε μια ομιλία του στη μαθηματική κοινότητα του Göttingen (Göttingen Mathematical Society) με τίτλο “Space and Time” (Διάστημα και χρόνος). Η ομιλία ξεκίνησε με τη φράση, σε ελεύθερη μετάφραση, “Εφεξής, ο χώρος και ο χρόνος ξεχωριστά θα είναι μια απλή “σκιά” και μόνο κάποια σύνδεση των δύο μπορεί να υπάρξει ανεξάρτητα” (“Henceforth, space for itself, and time for itself shall completely reduce to a mere shadow, and only some sort of union of the two shall preserve independence”).

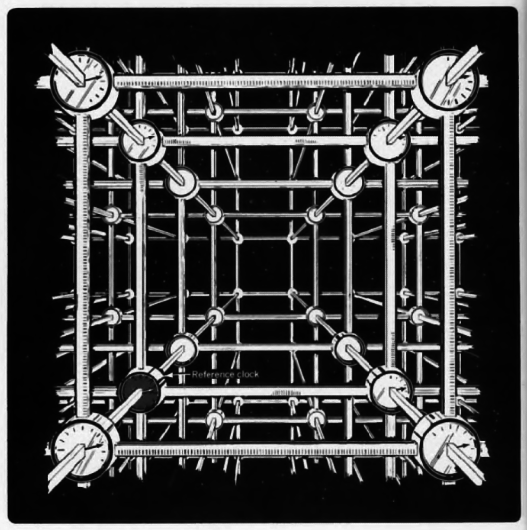
Η θεώρηση του χωρόχρονου (και συνεπώς των διαστάσεων) ως η νέα θεατρική σκηνή στην οποία τα γεγονότα συμβαίνουν, οδήγησε στην αντίληψη πως το ηλεκτρικό και το μαγνητικό πεδίο αποτελούν δύο εκφάνσεις της ίδιας οντότητας, δηλαδή του ηλεκτρομαγνητικού πεδίου. Επιπλέον, εξήγησε με ποιον τρόπο είναι δυνατή η σχάση και η σύντηξη των ατόμων, καθώς και πληθώρα άλλων φαινομένων.

Αυτή η όμορφη ιδέα της ενοποίησης, εξελίχθηκε περαιτέρω με την ταύτιση της καμπυλότητας του χωρόχρονου με τη βαρύτητα, μέσω της Γενικής Σχετικότητας. H γεωμετρικοποίηση της βαρύτητας αποτέλεσε την πηγή έμπνευσης για τους μαθηματικούς Kaluza και Klein, οι οποίοι εισήγαγαν μια πέμπτη διάσταση ώστε να ενοποιήσουν τη βαρύτητα με τον ηλεκτρομαγνητισμό. Με απλά λόγια, στις τέσσερις διαστάσεις, η βαρύτητα και ο ηλεκτρομαγνητισμός περιγράφονται από δύο διαφορετικά σύνολα εξισώσεων. Στις πέντε διαστάσεις των Kaluza και Klein θα μπορούσαν (θεωρητικά και με κάποιους μαθηματικούς περιορισμούς) να περιγράφονται με ένα σύνολο εξισώσεων. Η θεωρία τους, παρόλο που πλέον έχει εγκαταλειφθεί λόγω θεωρητικών ασυνεπειών, αποτέλεσε τον προ-γεννήτορα της θεωρίας χορδών (Η βασική ιδέα της θεωρίας χορδών είναι πως όλα τα υποατομικά σωματίδια, όπως για παράδειγμα ηλεκτρόνια και νετρίνα, αποτελούν εκφάνσεις του ίδιου αντικειμένου, της χορδής. Η διαφορετικότητά των σωματιδίων βασίζεται στους τρόπους ταλάντωσης της χορδής, στο αν είναι κλειστή ή ανοιχτή και σε άλλες ιδιότητες.)

Υπάρχουν διαφορετικές θεωρίες χορδών, οι οποίες απαιτούν επιπλέον διαστάσεις για τη μαθηματική τους συνέπεια. Μερικά παραδείγματα είναι η μποζονική θεωρία χορδών, η οποία απαιτεί 26 διαστάσεις, η θεωρία υπερ-χορδών 10 διαστάσεις και η M-theory 11 διαστάσεις. Όσες επιπλέον διαστάσεις και να υπάρχουν, αυτές θα πρέπει με κάποιο τρόπο να παραμένουν μη παρατηρήσιμες στις ενεργειακές κλίμακες της καθημερινότητάς μας. Αυτό οδήγησε σε μαθηματικές κατασκευές όπως είναι οι πολλαπλότητες Calabi-Yau, οι οποίες περιγράφουν γεωμετρικά τις επιπλέον διαστάσεις.

Πως όμως θα μπορούσαν να επιβεβαιωθούν πειραματικά οι επιπλέον διαστάσεις;

Ένα όμορφο παράδειγμα δίνεται στο βιβλίο του Barton Zwiebach (A First Course in String Theory), όπου μελετάται ένας από τους τρόπους που αλλάζει η βαρυτική δύναμη του Νεύτωνα λόγω της ύπαρξης επιπλέον διαστάσεων. Μέχρι στιγμής, με πειράματα αυτού του είδους (τύπου Eötvos), για δύο σώματα σε απόσταση τάξης εκατοστών, η Νευτώνεια θεωρία επιβεβαιώνεται μέχρι και τάξη 10^-4. Επομένως, αν υπάρχουν συμπαγείς επιπλέον διαστάσεις θα πρέπει να έχουν μέγεθος μικρότερο τους ενός δεκάτου του χιλιοστού. Άλλου είδους πειράματα είναι εκείνα που διεξάγονται στο CERN και αναζητούν κάποια παραβίαση της διατήρησης της ενέργειας ή/και της ορμής στις αλληλεπιδράσεις των σωματιδίων.

Εν κατακλείδι, μέχρι και σήμερα η ύπαρξη επιπλέον διαστάσεων δεν έχει επιβεβαιωθεί πειραματικά. Η οποιαδήποτε πειραματική απόδειξη, θα ερμηνευθεί σε μαθηματικό επίπεδο ως αλλαγή στους φυσικούς νόμους οι οποίοι ισχύουν έως και σήμερα.

Μερικά ενδιαφέροντα συγγράμματα

1. On the Electrodynamics of moving bodies, Albert Einstein, Translated by George Barker Jeffery; Wilfrid Perrett. London: Methuen and Company, Ltd.

2. A First Course in String Theory, Barton Zwiebach, Cambridge University Press, 2004.

3. Spacetime Physics, Edwin Taylor and Archibald Wheeler; W. H. Freeman 2nd edition (March 15, 1992).