Μπορούν τα βαρυτικά κύματα να μας φανερώσουν πόσο βαρείς είναι οι αστέρες νετρονίων;

Ποιά είναι η μεγαλύτερη μάζα που μπορεί να έχει ένας αστέρας νετρονίων πριν καταρρεύσει σε μία μαύρη τρύπα; Πρόσφατες παρατηρήσεις βαρυτικών κυμάτων προσφέρουν περισσότερες πληροφορίες.

Βρίσκοντας το Μέγιστο

Τα αστέρια νετρονίων αποτελούνται σχεδόν εξ’ ολοκλήρου από νετρόνια και έχουν τρομερές πυκνότητες, της τάξης μεγέθους της πυκνότητας της ύλης στους πυρήνες των ατόμων. Αυτή η ακραία μάζα σε έναν τόσο μικρό χώρο οδηγεί σε μια ισχυρή βαρυτική έλξη προς τα μέσα, που αυξάνεται καθώς στριμώχνονται όλο και περισσότερα νετρόνια. Όταν η δύναμη βαρύτητας υπερβαίνει τις συνδυασμένες κβαντικές και πυρηνικές δυνάμεις που ασκούν μια πίεση προς τα έξω, το αστέρι καταρρέει για να σχηματίσει μια μαύρη τρύπα.

Ποια είναι η μέγιστη μάζα, πάνω από την οποία ένα αστέρι νετρονίων καταρρέει; Η θεωρία μας λέει, πως για ένα μη-περιστρεφόμενο αστέρα νετρονίων, η μάζα αυτή κυμαίνεται κάπου ανάμεσα σε 2 με 3 ηλιακές μάζες – αλλά η ακριβής τιμή εξαρτάται από την άγνωστη κατάσταση της ύλης στο εσωτερικό του. Για να προσπεράσουμε την ελλιπή αυτή γνώση, χρειαζόμαστε παρατηρησεις που μπορούν να μας βοηθήσουν να θέσουμε περιορισμούς στο “βάρος” ενός αστέρα νετρονίων.

Πληροφορίες από συγκρούσεις

Τα τελευταία χρόνια, τα βαρυτικά κύματα μας έχουν δώσει πολύ χρήσιμες πληροφορίες. Ιδιαίτερα δύο συγκεκριμένες συγχωνεύσεις συμπαγών σωμάτων:

1. GW170817
   Στο γεγονός αυτό, δύο άστρα νετρονίων με μάζες 1.1-1.6 της μάζας το Ήλιου, συγχωνεύτηκαν για να δημιουργήσουν ένα μεγαλύτερο σώμα, που πιστεύουμε ότι κατέρρευσε σε μία μαύρη τρύπα, λίγο μετά τη σύγκρουση. Η ταυτόχρονη παρατήρηση βαρυτικών και ηλεκτρομαγνητικών κυμάτων από τα παραπάνω στάδια φανερώνει μια μέγιστη μάζα για τα άστρα νετρονίων που είναι μικρότερη από 2.3 ηλιακές μάζες.
   
   
2. GW190814
   Στο γεγονός αυτό, μια μαύρη τρύπα με μάζα μεγαλύτερη από 20 ηλιακές μάζες συγχωνεύτηκε με ένα αντικείμενο μάζας μόλις 2.5-2.7 της μάζας του Ήλιου – αλλά δε γνωρίζουμε αν το μικρότερο σώμα είναι μια μαύρη τρύπα ή αστέρας νετρονίων. Αν ήταν ένας, μη-περιστρεφόμενος αστέρας νετρονίων, αυτό θα σήμαινε ότι το μέγιστο όριο για τις μάζες των τελευταίων είναι παραπάνω από 2.5 ηλιακές μάζες.

Μπορούμε να συμβιβάσουμε τις δύο αυτές φαινομενικά αντικρουόμενες παρατηρήσεις; Μια μελέτη, καθοδηγούμενη από τον Αντώνιο Ναθαναήλ (Ινστιτούτο Θεωρητικής Φυσικής, Γερμανία) παρουσιάζει έναν νέο τρόπο ανάλυσης των παραπάνω συγχωνεύσεων που μας δίνει περαιτέρω πληροφορίες για τα μέγιστα όρια μάζας ενός αστέρα νετρονίων.

Ένα Ελάχιστο Μέγιστο Όριο

Ο Αντώνης Ναθαναήλ με συνεργάτες του ανέλυσαν τις δύο συγχωνεύσεις με έναν “γενετικό αλγόριθμο” – έναν αλγόριθμο που εξερευνά έναν μεγάλο χώρο παραμέτρων και ψάχνει να βρει τις βέλτιστες λύσεις με μία μέθοδο που μοιάζει με τη φυσική επιλογή. Με τον αλγόριθμο αυτό, οι συγγραφείς βρήκαν τις μέγιστες μάζες που είναι συνεπείς με τις βαρυτικές και ηλεκτρομαγνητικές παρατηρήσεις των GW170817 και GW190814 και με αριθμητικές προσομοιώσεις τέτοιων συγκρούσεων.

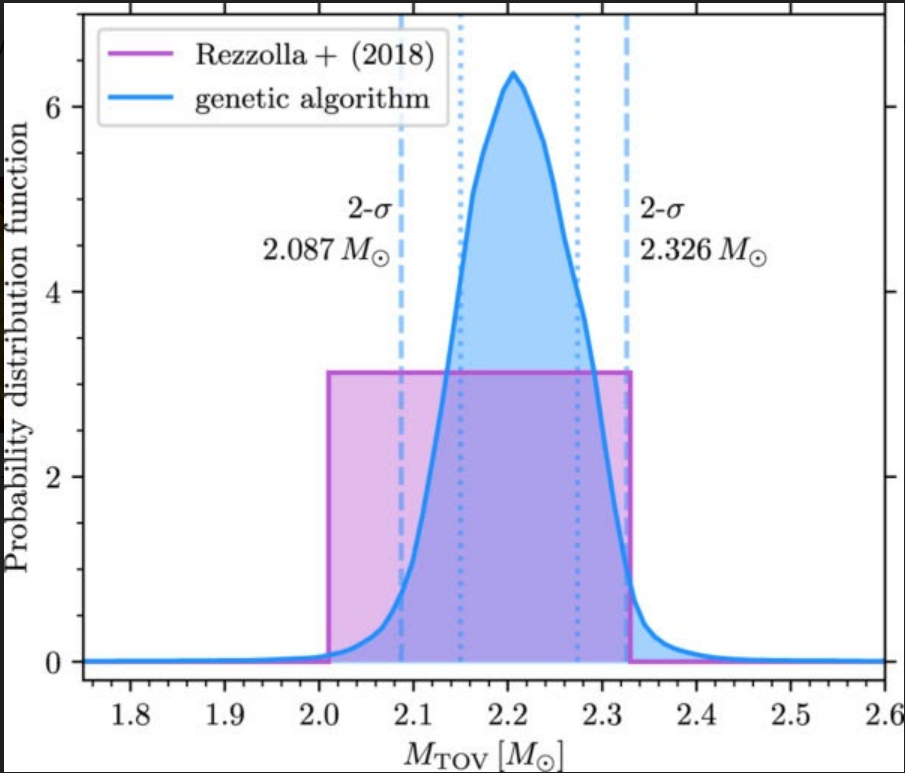
Η έρευνα τους δείχνει ότι μια μεγάλη μέγιστη μάζα αστέρων νετρονίων – όπως οι 2.5 ηλιακές μάζες που απαιτούνται εάν το δευτερεύον σώμα του GW190814 ήταν όντως ένα μη-περιστρεφόμενο αστέρι νετρονίων – δεν ταιριάζει με τις προσδοκίες για τη μέγιστη δυνατή μάζα, με βάση τα αποτελέσματα για το GW170817 ή αυτές των αριθμητικών προσομοιώσεων βαρυτικών κυμάτων

Ωστόσο, βρίσκουν ότι μια μέγιστη μάζα αστέρων νετρονίων περίπου 2.2 ηλιακών μαζών, αναπαράγει παράλληλα και τους παρατηρησιακούς περιορισμούς από το γεγονός GW170817 και συμφωνεί με τις αριθμητικές προσομοιώσεις. Αυτό το ανώτερο όριο υποδηλώνει ότι το δευτερεύον σώμα του GW190814 ήταν πολύ μεγάλο για να ήταν ένα μη-περιστρεφόμενο αστέρι νετρονίων. Με αποτέλεσμα, καταλήγουν ότι το GW190814 ήταν πιθανώς η συγχώνευση δύο μελανών οπών άνισης μάζας.

Πηγή: https://aasnova.org/2021/03/10/gravitational-waves-shed-light-on-how-heavy-a-neutron-star-can-be/

Περαιτέρω διάβασμα:

Στο άρθρο “GW170817 and GW190814: Tension on the Maximum Mass,” Antonios Nathanail et al 2021 ApJL 908 L28. doi:10.3847/2041-8213/abdfc6