Γιατί χρησιμοποιούμε «παράξενες» μονάδες στην (Αστρο)φυσική; – Μέρος Β

Στο πρώτο μέρος αυτού του άρθρου περιγράψαμε την ανάγκη εισαγωγής ορισμένων ιδιαίτερων  μονάδων μέτρησης στη Φυσική (και ειδικότερα στον κλάδο της Αστροφυσικής) και είδαμε ορισμένες από τις πιο συνηθισμένες. Με τον τρόπο αυτό μπορούμε να εκφράσουμε μεγάλες κλίμακες αποστάσεων, μεγάλες μάζες κλπ. Τι γίνεται όμως όταν θέλουμε να μελετήσουμε πολύ μικρές κλίμακες ενός φυσικού μεγέθους;

Ας ξεκινήσουμε πάλι με κάποια παραδείγματα από την καθημερινή μας ζωή. Οι συνταγές των αγαπημένων σας φαγητών χρησιμοποιούν κιλά (kg) ή γραμμάρια (g) για το βάρος (ή πιο σωστά, τη μάζα) του κάθε συστατικού. Θα έχετε προσέξει όμως πως η δραστική ουσία ενός φαρμάκου εκφράζεται συνήθως σε mg (μιλιγκράμ, δηλαδή ένα χιλιοστό του γραμμαρίου) ή ακόμα και μg (μικρογραμμάρια, δηλαδή ένα εκατομμυριοστό του γραμμαρίου) – θα ήταν δύσκολο να εκφράσουμε τις τιμές αυτές με κιλά. Για τον ίδιο λόγο, όταν αναφερόμαστε σε μικρές τιμές μήκους χρησιμοποιούμε χιλιοστά του μέτρου (mm) ή εκατομμυριοστά του μέτρου (μικρόμετρα – μm). Θα έχετε ακούσει ίσως για τα νανοϋλικά. Το όνομά τους οφείλεται στη διάσταση της θεμελιώδους δομικής μονάδας τους, η οποία έχει τυπικά διαστάσεις μερικά δισεκατομμυριοστά του μέτρου (νανόμετρα – nm). Δείτε ορισμένα παραδείγματα μικρών διαστάσεων και νανοϋλικών στην παρακάτω εικόνα:

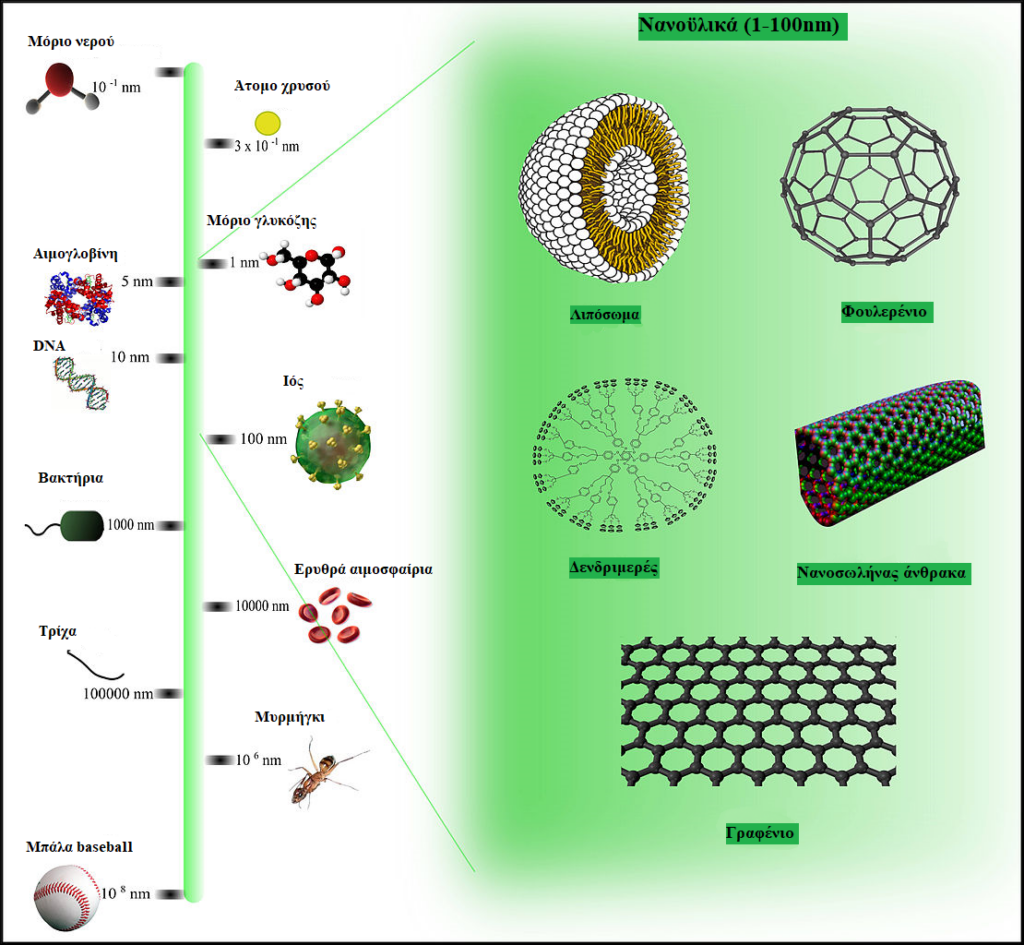
Στην ατομική και πυρηνική φυσική, οι κλίμακες μήκους είναι ακόμα μικρότερες. Το πιο απλό άτομο στον περιοδικό πίνακα, το υδρογόνο, έχει μέγεθος¹ περίπου 0,05 νανόμετρα, ενώ τα μεγέθη των πυρήνων είναι έως και δέκα χιλιάδες φορές μικρότερα. Για το λόγο αυτό συνήθως χρησιμοποιούμε ως μονάδα μέτρησης μήκους το Ångström (ίσο με 0,1 δισεκατομμυριοστά του μέτρου) για τα μεγέθη των ατόμων και μια υποδιαίρεση του μέτρου γνωστή ως femtometre για μεγέθη πυρήνων. Ένα femtometre ισούται με ένα τετράκις εκατομμυριοστό του μέτρου, δηλαδή το μηδέν ακολουθούμενο από υποδιαστολή, δεκατέσσερα μηδενικά και το ψηφίο 1!

Η μονάδα ηλεκτρικού φορτίου του SI, το Coulomb (Cb) είναι περίπου 10¹⁹ (1 ακολουθούμενο από 19 μηδενικά!) φορές μεγαλύτερη από το στοιχειώδες φορτίο ενός ηλεκτρονίου ή ενός πρωτονίου (αγνοώντας το πρόσημο). Για το λόγο αυτό, όταν μελετάμε φορτισμένα σωματίδια, εκφράζουμε το φορτίο τους ως πολλαπλάσιο του φορτίου του ηλεκτρονίου, με το κατάλληλο πρόσημο (+ για θετικά φορτισμένα, – για αρνητικά φορτισμένα σωματίδια). Αν ένα άτομο οξυγόνου χάσει ένα ηλεκτρόνιο (γίνει δηλαδή ένα θετικό ιόν), έχει φορτίο +1.

Τέλος, ας ασχοληθούμε με την ενέργεια. Η μονάδα μέτρησης ενέργειας στο SI είναι το Joule (J). Στην καθημερινή μας ζωή ωστόσο χρησιμοποιούμε κιλοβατώρες για την κατανάλωση ηλεκτρικής ενέργειας στα σπίτια μας και θερμίδες για την ενέργεια που μας προσφέρει ένα τρόφιμο. Σίγουρα δύο λέξεις που έχουν φορτιστεί… αρνητικά! Και οι 3 μονάδες αυτές είναι αρκετά άβολες για να περιγράψουμε ενέργειες στην πυρηνική φυσική. 

Ορίζουμε λοιπόν μια νέα, χρήσιμη μονάδα, το ηλεκτρονιοβόλτ (eV), που περιγράφει την ενέργεια που θα αποκτήσει ένα αρχικά ακίνητο ηλεκτρόνιο αν βρεθεί σε διαφορά δυναμικού (“τάση”) ενός βολτ (V). Η μονάδα αυτή είναι εξαιρετικά μικρή², περίπου ίση με 1,6 ⋅10^-19 J (δοκιμάστε να το γράψετε: μηδέν, υποδιαστολή, 18 μηδενικά και ο αριθμός 16). 

Στην πυρηνική φυσική, οι εξαιρετικά μικρές μάζες των στοιχειωδών σωματιδίων συχνά εκφράζονται μέσω της ενέργειας, χρησιμοποιώντας τη διάσημη εξίσωση του Einstein E = mc². Στην εξίσωση αυτή, m είναι η μάζα “ηρεμίας” (όταν το σωματίδιο είναι ακίνητο), c η ταχύτητα του φωτός και Ε η “ισοδύναμη” ενέργεια. Έτσι, λέμε ότι το πρωτόνιο (με μάζα ηρεμίας 1,6 ⋅10^-27 kg περίπου) έχει “μάζα” σχεδόν 1 GeV (1 δισεκατομμύριο ηλεκτρονιοβόλτ), ενώ το ηλεκτρόνιο (με μάζα ηρεμίας 9,1 ⋅10^-31 kg περίπου) έχει “μάζα” σχεδόν 511 χιλιάδες ηλεκτρονιοβόλτ. Στην πραγματικότητα όμως, εκφράζουμε την ενέργεια διαιρεμένη με την ταχύτητα του φωτός στο τετράγωνο.

Ο κατάλογος των μονάδων μέτρησης ωστόσο δεν τελειώνει εδώ! Όχι μόνο έχουμε παραλείψει ν’ αναφέρουμε αρκετά φυσικά μεγέθη, αλλά ακόμα και στον ίδιο τομέα έρευνας εμφανίζονται συχνά διαφορετικές κλίμακες. Συνεπώς, ο κάθε ερευνητής καλείται συχνά να απλοποιήσει τους υπολογισμούς του, χρησιμοποιώντας “τυπικές” κλίμακες που εμφανίζονται στο πρόβλημα που μελετάει. 

¹ Ως μέγεθος εδώ θα θεωρήσουμε την πιο πιθανή απόσταση του ηλεκτρονίου στο άτομο του υδρογόνου από τον πυρήνα, με άλλα λόγια την “ακτίνα” του ατόμου.

² Αν θέλατε να εκφράσετε τις θερμίδες που σας προσφέρουν 100gr σοκολάτας γάλακτος σε ηλεκτρονιοβόλτ, ετοιμαστείτε να απογοητευτείτε, αφού θα πρέπει να γράψετε τον αριθμό 13 με 24 μηδενικά!