Πόσα χρόνια θα χρειαζόντουσαν για να επισκεφτεί κάποιος ταξιδιώτης υποθετικά όλους τους γαλαξίες του ορατού Σύμπαντος;

Δυστυχώς η απάντηση αυτή είναι απλή και… πολύ απογοητευτική! Είναι αδύνατον ένας ταξιδιώτης, με την τεχνολογία που διαθέτουμε σήμερα (ή θα αποκτήσουμε στο άμεσο μέλλον) να ταξιδέψει σε όλο το Σύμπαν. Θα προσπαθήσουμε σε αυτό το άρθρο να εξηγήσουμε το γιατί, αλλά και να εξερευνήσουμε ορισμένες περιπτώσεις στις οποίες ένα ταξίδι θα ήταν σχετικά “εφικτό”.

Το βασικό πρόβλημα, το οποίο εμφανίζεται συχνά σε τέτοιες ερωτήσεις, είναι οι τεράστιες αποστάσεις στο Σύμπαν και η μικρή ταχύτητα που μπορεί να έχει ένα διαστημόπλοιο, σε σχέση με την ταχύτητα του φωτός στο κενό (τη μέγιστη ταχύτητα κατά τους γνωστούς νόμους φυσικής – δείτε σχετικά εδώ). 

Επιπλέον, το Σύμπαν δεν είναι στατικό αλλά διαστέλλεται. Επομένως, όταν ξεκινήσουμε το ταξίδι μας στους γαλαξίες, η απόσταση που θα έχουμε να διανύσουμε ολοένα και θα αυξάνεται. Αν μάλιστα ο ρυθμός διαστολής είναι μεγαλύτερος από την ταχύτητα του διαστημοπλοίου μας, τότε η απόσταση μεταξύ των γαλαξιών θα μεγαλώνει πιο γρήγορα από την απόσταση που καλύπτουμε στο ταξίδι μας. Μπροστά μας θα έχουμε ένα γαλαξιακό δρόμο που μεγαλώνει επ’ άπειρον.

Ας δούμε όμως κάποιες απλοποιημένες εκδοχές της ερώτησης-προβλήματος. Σημειώνουμε στο σημείο αυτό ότι οι παραδοχές που θα κάνουμε δεν είναι -αυστηρά μιλώντας- ρεαλιστικές, αλλά μπορούν, σε κάποιο βαθμό, να δώσουν ορισμένες διαισθητικές απαντήσεις. 

Ας περιορίσουμε αρχικά την έρευνά μας στο Τοπικό Σύμπλεγμα Γαλαξιών (Local Group) και ας υποθέσουμε ότι οι αποστάσεις μεταξύ των γαλαξιών που το αποτελούν είναι σταθερές (ή τουλάχιστον αλλάζουν πολύ αργά σε σύγκριση με το χρόνο του ταξιδιού μας). Αν και μπορούμε να επισκεφτούμε τους γαλαξίες με όποια σειρά θέλουμε, συμφέρει να βρούμε τη συντομότερη χρονικά διαδρομή. Ένα διάσημο ανάλογο πρόβλημα είναι το πρόβλημα του περιπλανώμενου εμπόρου, στο οποίο ο έμπορος πρέπει να επισκεφτεί έναν αριθμό από πόλεις στον ελάχιστο χρόνο. Η λύση αυτού του προβλήματος είναι πολύ δύσκολη για κάθε συγκεκριμένη κατανομή γαλαξιών, αλλά εφόσον έχουμε να κάνουμε με πάρα πολλές κατανομές, πρακτικά τυχαίες στις διαρρυθμίσεις τους, μπορούμε να κάνουμε μία απλοποίηση για την ευχέρεια των υπολογισμών μας. 

Ας υποθέσουμε ότι έχουμε ένα σύμπλεγμα γαλαξιών. Εάν οι γαλαξίες που το αποτελούν είναι ομοιόμορφα κατανεμημένοι, η μέση απόσταση μεταξύ τους υπολογίζεται μέσω της ακτίνας του συμπλέγματος και του αριθμού των γαλαξιών που τον αποτελούν (συγκεκριμένα, βρίσκεται πως είναι δύο φορές η ακτίνα του συμπλέγματος προς την τρίτη ρίζα του αριθμού γαλαξιών). Λόγω ομοιομορφίας, ο συνολικός χρόνος δεν είναι παρά το άθροισμα όλων των μέσων χρόνων ταξιδιού ανάμεσα στους γειτονικούς γαλαξίες. Με περίπου 100 γαλαξίες σε ένα τυπικό σύμπλεγμα ακτίνας 1 Mpc¹, εάν μπορούμε να ταξιδέψουμε με την ταχύτητα του φωτός, ο χρόνος “τουρισμού” θα είναι περίπου εκατό εκατομμύρια χρόνια.

Το ορατό σύμπαν έχει περίπου ένα τρισεκατομμύριο γαλαξίες, σε τάξη μεγέθους. Σε αυτό το σημείο μπορούμε να αξιοποιήσουμε την αυτο-ομοιότητα του Σύμπαντος. Οι δομές των γαλαξιών στα συμπλέγματά τους κατά κάποιο τρόπο επαναλαμβάνονται, σε μεγαλύτερη κλίμακα, στα υπερσυμπλέγματα². Εάν υποθέσουμε ότι αυτό γίνεται με εντελώς όμοιο τρόπο, δηλαδή σε κάθε βήμα έχουμε 100 φορές από ότι είχαμε στο προηγούμενο, μπορούμε να επαναλάβουμε αυτή τη διαδικασία, πολλαπλασιαστικά, πέντε ακόμα φορές, ώστε να φτάσουμε στην τελική δομή, με περίπου ένα τρισεκατομμύριο γαλαξίες. Αυτό σημαίνει ότι μπορούμε να δοκιμάσουμε να το επισκεφθούμε όλο με έξι βήματα αυξανόμενης κλίμακας, καθένα από τα οποία περιέχει 100 δείγματα από το προηγούμενο. Ο συνολικός χρόνος για κάθε καινούργια δομή θα υπολογίζεται όπως πριν, για την ακτίνα της κάθε δομής, συν το χρόνο ταξιδιού μεταξύ όλων των παρακάτω δομών. 

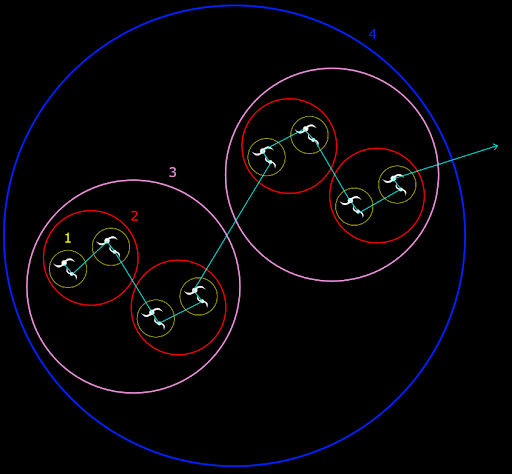
Κάνοντας τους υπολογισμούς γρήγορα προκύπτει ότι ο συνολικός χρόνος που δαπανάται εντός των χαμηλότερων δομών είναι πολύ περισσότερος από το χρόνο ταξιδιού μεταξύ αυτών των δομών, οπότε σε κάθε κλίμακα ο συνολικός χρόνος είναι περίπου 100 φορές μεγαλύτερος. Συνολικά, για επίσκεψη σε ένα τρισεκατομμύριο γαλαξίες σε ένα ορατό σύμπαν με διάμετρο περίπου 10000 Mpc, θα χρειαστούν ένα δισεκατομμύριο δισεκατομμύρια χρόνια. 

Τι γίνεται όμως με τη διαστολή του Σύμπαντος; Αυτή περιγράφεται με τη σταθερά του Hubble, που είναι περίπου 70 km ανά δευτερόλεπτο ανά Mpc. Αυτό σημαίνει ότι κάθε δευτερόλεπτο, σημεία που απέχουν 1 Mpc απομακρύνονται το ένα από το άλλο επιπλέον 70 km (περίπου – υπάρχει κάποια αβεβαιότητα για την ακριβή τιμή, μεταξύ 67 και 74). Εάν το εφαρμόσουμε αυτό στο αρχικό σύμπλεγμα γαλαξιών μας, θα δούμε ότι στη διάρκεια του ταξιδιού μας (εκατό εκατομμύρια χρόνια), η διάμετρός του, που ήταν αρχικά 2 Mpc, θα έχει αυξηθεί κατά περίπου δύο εκατοστά του Mpc (0.02 Mpc). Είναι μία αμελητέα επίπτωση για τους υπολογισμούς μας. Τα πράγματα, όμως, αλλάζουν για τις μεγαλύτερες κλίμακες.

Στη δεύτερη κιόλας κλίμακα μεγέθους τα πράγματα γίνονται σοβαρότερα. Πλέον η απόσταση είναι έξι φορές μεγαλύτερη και ο χρόνος είναι εκατό φορές μεγαλύτερος. Έτσι βρίσκουμε ότι μέχρι να γυρίσουμε όλο το υπερσύμπλεγμα των εκατό συμπλεγμάτων, η διάμετρός του θα έχει διπλασιαστεί! Αυτό δεν αλλάζει ορατά το αποτέλεσμα χρόνου καθότι, όπως είπαμε, αυτό βασίζεται κυρίως στον μεγάλο αριθμό των συμπλεγμάτων και όχι στην ακτίνα του υπερσυμπλέγματος. Όμως, όταν πηγαίνουμε σε μεγαλύτερες κλίμακες μεγέθους, σε κάθε μεγαλύτερη κλίμακα η επίδραση της διαστολής γίνεται εκατό φορές ισχυρότερη από ότι στην προηγούμενή της, οπότε στην τελευταία κλίμακα η ακτίνα της θα έχει γίνει εκατό εκατομμύρια φορές μεγαλύτερη μέχρι το υποθετικό τέλος του ταξιδιού. Αυτό εκατονταπλασιάζει το συνολικό χρόνο ταξιδιού, που με τη σειρά του εκατονταπλασιάζει τη διαστολή, και ούτω καθεξής. Το ταξίδι γίνεται άπειρο και έτσι ανέφικτο³.

¹ Ένα Mpc ισούται με ένα εκατομμύριο parsec. Ένα parsec είναι 3,26 έτη φωτός ή περίπου 30 τρισεκατομμύρια χιλιόμετρα.

² Ίσως σας βοηθήσουν οι προσομοιώσεις που παρουσιάζονται εδώ: https://icc.dur.ac.uk/Eagle/

³ Πόσο μάλλον αν λάβουμε υπόψη ότι η διαστολή του σύμπαντος επιταχύνεται. Η σταθερά του Hubble δεν είναι καθόλου σταθερά σε βάθος χρόνου. 

Συγγραφείς: Σταύρος Δημητρακούδης και Δημήτρης Μήλλας