Οπτική απόκριση των μετάλλων

Σε προηγούμενο άρθρο αναφερθήκαμε στις τεχνολογικές δυνατότητες που προσφέρουν μεταλλικά συστήματα εξαιρετικά μικρών διαστάσεων, της τάξης των μερικών δεκάδων νανομέτρων, τόσο στην ιατρική και τη χημεία, όσο και στην οπτική (από την οποία ο γράφων βγάζει τα προς το ζειν, οπότε έχει μεγαλύτερο ενδιαφέρον). Είδαμε ότι η διέγερση πλασμονίων, ταλαντώσεων δηλαδή των ελεύθερων ηλεκτρονίων του μετάλλου που διεγείρονται από την προσπίπτουσα ηλεκτρομαγνητική ακτινοβολία, παίζει καθοριστικό ρόλο στην οπτική τους απόκριση. Τι σημαίνει όμως ελεύθερα ηλεκτρόνια, και πώς διεγείρονται εξωτερικά με ένα συνηθισμένο laser;

Για να δώσουμε την απάντηση, θα μεταφερθούμε 125 χρόνια πίσω, για να παρακολουθήσουμε μια πολύ διδακτική ιστορία. Είμαστε στα 1897, και ο Joseph Thomson βρίσκεται στο εργαστήριό του στο Cambridge και έκπληκτος παρατηρεί τις καθοδικές ακτίνες (ακτίνες που παράγονταν από τη σύγκρουση θετικών ιόντων με ένα μεταλλικό αρνητικό ηλεκτρόδιο, Εικόνα 1) που έστελνε σε ένα στόχο να αλλάζουν πορεία όταν βρίσκονταν μέσα σε ηλεκτρικό πεδίο, και να συμπεριφέρονται σαν να είναι αρνητικά φορτισμένα σωματίδια. Την εποχή εκείνη οι επιστήμονες είχαν ήδη καλή γνώση του ηλεκτρισμού, και μπορούσαν να πουν ότι τα ηλεκτρικά ρεύματα οφείλονται σε κινούμενα φορτία, αλλά δεν είχαν ιδέα για τη φύση αυτών των φορτίων. Και ξαφνικά διαπίστωσαν την ύπαρξη αρνητικών φορτίων, τα οποία μάλιστα, με βάση τις τροχιές τους στο παραπάνω πείραμα, υπολογίστηκε ότι έχουν μάζα περίπου 2000 φορές μικρότερη από αυτή ενός ιόντος υδρογόνου (θετικά ιόντα είχαν ήδη παρατηρηθεί, αλλά καθώς προερχόταν από διαφορετικά άτομα, είχαν διαφορετικούς αριθμούς πρωτονίων, οπότε ασφαλή συμπεράσματα δεν ήταν εύκολο να προκύψουν). Λόγω αυτής της διαφοράς μαζών, ο Thomson πρότεινε ένα ατομικό μοντέλο που θύμιζε σταφιδόψωμο: ένα μεγάλο θετικό ψωμάκι, και πολλές αρνητικά φορτισμένες σταφίδες διάσπαρτες στο εσωτερικό και την επιφάνειά του (Εικόνα 2).

  Η ανακάλυψη αυτή είχε εκπληκτικές συνέπειες για τη φυσική, και κατ’ επέκταση τη ζωή μας εν γένει. Ανάμεσα στα άλλα πεδία που επηρεάστηκαν, ήταν και η φυσική στερεάς κατάστασης (η οποία, μεταξύ μας, ουσιαστικά δεν υπήρχε εκείνη την εποχή). Οι επιστήμονες γνώριζαν ότι κάποια υλικά, τα μέταλλα, έχουν διαφορετικές ιδιότητες από άλλα: έχουν πολύ μεγαλύτερη ηλεκτρική και θερμική αγωγιμότητα. Το γιατί, ωστόσο, ήταν άγνωστο. Σκεφτείτε λοιπόν πόσο σημαντική ήταν η ανακάλυψη ενός φοβερά ελαφριού αρνητικά φορτισμένου σωματιδίου, που λογικά θα πρέπει να βρίσκεται σε όλα τα άτομα, ώστε να είναι ηλεκτρικά ουδέτερα! Υπάρχουν πλέον τα κινούμενα φορτία που χρειαζόμαστε για ένα ρεύμα. Εφαρμόζοντας λοιπόν μόνο αυτά που ήξερε (βασικά κλασική μηχανική και θερμοδυναμική), ο Paul Drude, καθηγητής στη Λειψία, μόλις 3 χρόνια αργότερα πρότεινε ένα ιδιαίτερα πετυχημένο μοντέλο για να περιγράψει τα μέταλλα και να εξηγήσει τις ιδιότητές τους. Ας σκεφτούμε μια επέκταση του σταφιδόψωμου του Thomson, με τον κυρίως όγκο του μετάλλου να παίζει το ρόλο του ζυμαριού, και κάποια ηλεκτρόνια να κινούνται ελεύθερα μέσα σε αυτό. Ουσιαστικά μια σούπα ηλεκτρονίων, αυτό που ακόμα και σήμερα αποκαλούμε ηλεκτρονικό αέριο. Πώς θα συμπεριφερθούν αυτά τα ηλεκτρόνια; Μα όπως κάθε άτομο αερίου, θα κινούνται ευθύγραμμα μέχρι να συγκρουστούν με ένα άλλο ηλεκτρόνιο ή ένα ιόν και να αλλάξουν πορεία (Εικόνα 3 – στο μοντέλο του Drude, οι κρούσεις μεταξύ ηλεκτρονίων θεωρούνται αμελητέες λόγω μεγέθους). Παρουσία ενός σταθερού ηλεκτρικού πεδίου (μιας τάσης), θα κινηθούν οργανωμένα οδηγώντας σε ένα ηλεκτρικό ρεύμα, ενώ η κίνησή τους και οι συγκρούσεις τους αντιστοιχούν σε θερμότητα. Έχουμε λοιπόν ηλεκτρική και θερμική αγωγιμότητα!

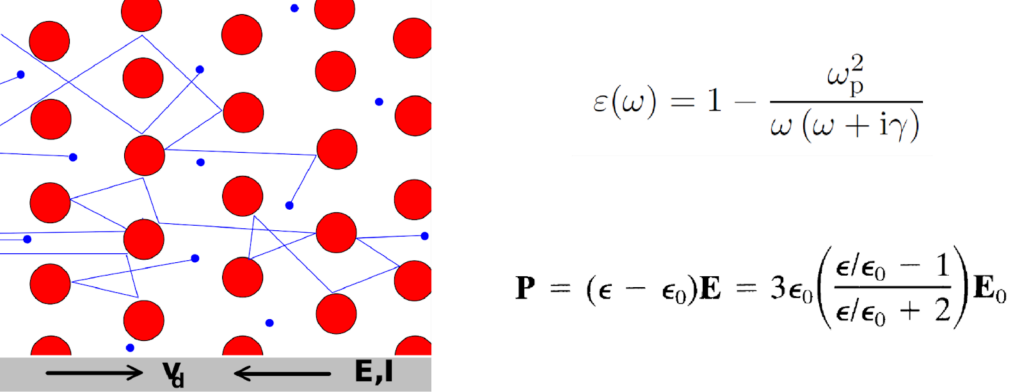
    Τι γίνεται όμως αν έχουμε ένα ταλαντούμενο ηλεκτρικό πεδίο, όπως αυτό μιας δέσμης φωτός; Και πάλι, τα ηλεκτρόνια ακολουθούν το πεδίο, δημιουργούν ένα ταλαντούμενο ηλεκτρικό ρεύμα το οποίο, αν το εισάγουμε στις τότε πρόσφατες (1862) εξισώσεις του Maxwell, οδηγούν στη διηλεκτρική συνάρτηση ε της Εικόνας 3: η απόκριση του μετάλλου σε ένα εξωτερικό πεδίο E δημιουργεί μια πόλωση P (μια συγκέντρωση φορτίων μέσα στο μέταλλο) που ακολουθεί την ταλάντωση της διέγερσης με συχνότητα ω, εξαρτάται από τη συγκέντρωση ηλεκτρονίων (μέσω της συχνότητας πλάσματος ω_p), και φθίνει λόγω κρούσεων με ρυθμό γ.

   Αυτό το φαινομενικά απλοϊκό μοντέλο αποδείχτηκε απίστευτα αποτελεσματικό, και 90-100 χρόνια αργότερα αποτέλεσε τη βάση για την περιγραφή των νανοδομών που κυριάρχησαν στα πρώτα χρόνια της άνθισης της πλασμονικής, με διαστάσεις της τάξης των 50-100 νανομέτρων: το μόνο που χρειαζόταν ήταν να λύσει κανείς τις εξισώσεις του Maxwell αναλυτικά ή αριθμητικά, χρησιμοποιώντας για την περιγραφή του μετάλλου είτε την απλή διηλεκτρική συνάρτηση ελεύθερων ηλεκτρονίων του Drude, είτε πειραματικά δεδομένα από ελλειψομετρία λεπτών επίπεδων μεταλλικών πλακιδίων. Σε ορισμένες περιπτώσεις μάλιστα, ούτε καν αυτό, μια και ένα μικρό νανοσωματίδιο μπορεί σε καλή προσέγγιση να θεωρηθεί ένα απλό ηλεκτρικό δίπολο (αν οι διαστάσεις του είναι αρκετά μικρότερες από το μήκος κύματος του φωτός), και η απόκρισή του να δοθεί από την απλή πόλωση της Εικόνας 3: η συνάρτηση Drude παίρνει αρνητικές τιμές, η διηλεκτρική συνάρτηση του περιβάλλοντος είναι θετική, οπότε υπάρχει συχνότητα στην οποία ο παρονομαστής μηδενίζεται και έχουμε οπτικούς συντονισμούς!

Η κατάσταση αυτή άρχισε ωστόσο να αλλάζει δραστικά στις αρχές της προηγούμενης δεκαετίας, οδηγούμενη και πάλι από την πρόοδο της νανοτεχνολογίας. Νανοδομές με διαστάσεις λίγων νανομέτρων, ή με μεταξύ τους αποστάσεις ακόμα και κάτω του νανομέτρου, είναι πλέον εφικτές. Σε αυτές τις περιπτώσεις η κλασική περιγραφή προέβλεπε έναν αφύσικο απειρισμό της ενίσχυσης του ηλεκτρικού πεδίου γύρω από τα σωματίδια, που βέβαια δε μετρήθηκε ποτέ πειραματικά. Έγινε λοιπόν σαφές ότι είχε έρθει η στιγμή να τροποποιηθεί η θεωρία, και να ληφθούν υπόψη στοιχεία από την κβαντομηχανική περιγραφή του μετάλλου (που αναπτύχθηκε εν τω μεταξύ μαζί με την ίδια την κβαντομηχανική και τη φυσική στερεάς κατάστασης), ανοίγοντας το δρόμο για το πεδίο της κβαντικής πλασμονικής, που θα αναλύσουμε σε επόμενο άρθρο.