Για την πληρέστερη κατανόηση της έννοιας των αρχικών συνθηκών χρειάζεται να “δούμε” τη μεγάλη εικόνα στην οποία αυτές εντάσσονται. Η εικόνα αυτή δεν είναι άλλη από το πεδίο των Διαφορικών Εξισώσεων (Συνήθων ή Μερικών) και της τεράστιας πολυμορφίας που αυτές παρουσιάζουν. Η ανάπτυξη του πεδίου των διαφορικών εξισώσεων συνέβαλε, συμβάδισε και αναπτύχθηκε παράλληλα με τη ραγδαία ανάπτυξη της Φυσικής τους προηγούμενους αιώνες. Οι διαφορικές εξισώσεις στη φύση, περιγράφουν την αλλαγή διαφόρων φυσικών μεγεθών με το χρόνο. 

Ένα απλό παράδειγμα συστήματος διαφορικών εξισώσεων για την πληρέστερη παρουσίαση του θέματος μπορούμε να πάρουμε από το πεδίο της πληθυσμιακής βιολογίας. Η εκθετική αύξηση ενός πληθυσμού δίνεται από την ακόλουθη διαφορική εξίσωση:

Η προηγούμενη εξίσωση μας λέει ότι ο ρυθμός μεταβολής ενός μεγέθους (στην προκειμένη περίπτωση του πληθυσμού) είναι ανάλογος του ίδιου του πληθυσμού. Για να μπορέσουμε να μελετήσουμε τη συμπεριφορά και την εξέλιξη του πληθυσμού θα πρέπει να ξέρουμε για κάποια χρονική στιγμή το μέγεθος του πληθυσμού. Αυτή την πληροφορία μας τη δίνουν οι αρχικές συνθήκες του προβλήματος. Ένα παράδειγμα αρχικών συνθηκών για το πρόβλημά μας θα μπορούσαν να είναι οι:

Η λύση της προηγούμενης διαφορικής εξίσωσης παρουσιάζεται στη συνέχεια για δύο διαφορετικές αρχικές συνθήκες. Στην πρώτη περίπτωση για X₀=0.5 και στη δεύτερη περίπτωση για X₀=0.5+0.001. Έχουμε επιλέξει κατάλληλα το α ώστε να είναι διακριτή η απόκλιση που παρουσιάζουν οι καμπύλες μας.

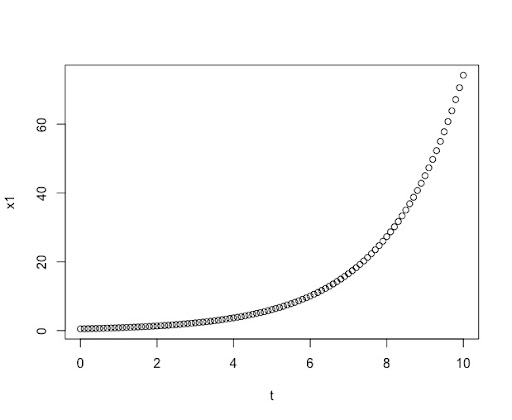
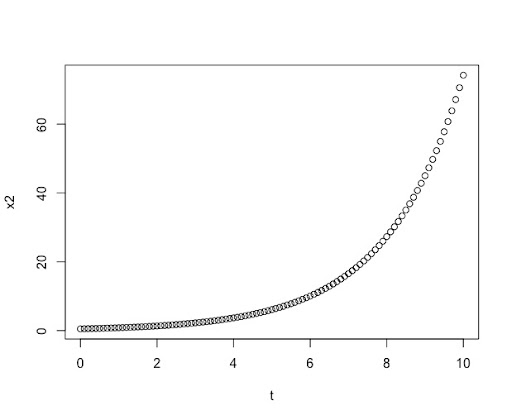
Εικόνα 1: Η λύση της διαφορικής εξίσωσης στο πρώτο γράφημα για αρχική συνθήκη X₀=0.5 ενώ στο δεύτερο για αρχική συνθήκη X₀=0.5+0.001. Οι διαφορές είναι σχεδόν ανύπαρκτες. Στην περίπτωση αυτή έχουμε επιλέξει ένα αυθαίρετο σύστημα απλά και μόνο για να αναδείξουμε την ευαισθησία στις αρχικές συνθήκες.

Αυτό που παρατηρούμε είναι ότι οι δύο γραφικές παραστάσεις παρουσιάζουν ασήμαντη έως μηδαμινή διαφορά ως προς τις αρχικές συνθήκες που δώσαμε. Λογική εξέλιξη αν σκεφτεί κάποιο ότι αλλάξαμε την αρχική συνθήκη κατά 0.001. Κοινώς κατά ένα χιλιοστό. Δε συμβαίνει το ίδιο όμως στην περίπτωση διαφορικών εξισώσεων που περιγράφουν χαοτικά φαινόμενα. Ας δούμε πως εξελισσόταν το απλοποιημένο σύστημα για τον καιρό από τις εκτυπώσεις που πήρε ο Lorenz το 1961.

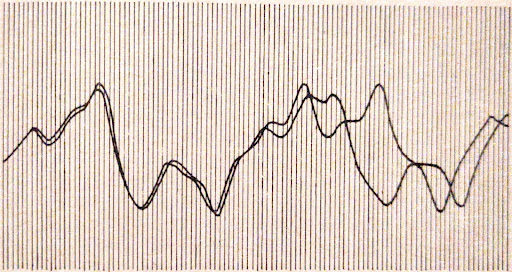
Παρατηρούμε ότι οι λύσεις ενώ στην αρχή ταυτίζονται (https://2science.gr/chaos/), γρήγορα διαχωρίζονται και φτάνουν να αποτελούν δύο διαφορετικές καμπύλες από τη μέση σχεδόν της γραφικής παράστασης. Οι διαφορές αυτές αντιστοιχούν σε διαφορετική ποιοτική συμπεριφορά για το σύστημα. Για την ιστορία η αλλαγή που έκανε ο Lorenz στις αρχικές συνθήκες ήταν να στρογγυλοποιήσει την αρχική τιμή 0.506127 που είχε δώσει σε 0.506!!! Μία τόσο μικρή αλλαγή στην αρχική συνθήκη προκάλεσε μία τόσο μεγάλη αλλαγή στη συμπεριφορά του συστήματος. 

Αν και σε ένα τέτοιο άρθρο δεν μπορούμε να σταθούμε εκτεταμένα στο εύρος εφαρμογών που αποτυπώνουν οι δύο προηγούμενες περιπτώσεις, αναδεικνύεται ωστόσο η σημασία που έχουν οι αρχικές συνθήκες στο σύστημα που εφαρμόζονται.