Φοράτε τη διαστημική σας στολή και με κάποιον μαγικό τρόπο ξεκινάτε το ταξίδι σας προς τη Σελήνη “περπατώντας” (είπαμε, με κάποιον μαγικό τρόπο!). Οπλιστείτε με υπομονή, το ταξίδι θα είναι αρκετά μεγάλο… Ακόμα και με συνεχόμενο “βάδισμα”, θα χρειαζόσασταν τουλάχιστον 10 χρόνια! Αν σας ενδιαφέρει να μάθετε πώς προέκυψε αυτή η απάντηση, καθώς και τις παραδοχές μας, συνεχίστε την ανάγνωση.

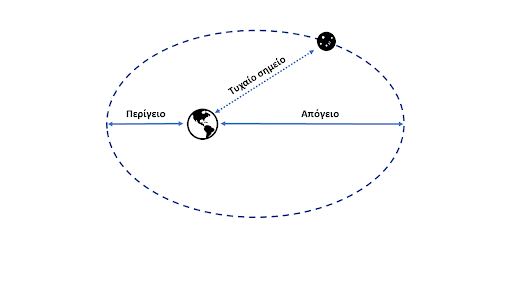
Θα ξεκινήσουμε με κάποια βασικά στοιχεία για την τροχιά της Σελήνης, η οποία είναι ελλειπτική, όπως φαίνεται στην Εικόνα 1. Το σημείο της τροχιάς με την ελάχιστη απόσταση από τη Γη (το περίγειο) απέχει περίπου 362 χιλιάδες χιλιόμετρα ενώ το σημείο με τη μέγιστη¹ (το απόγειο) περίπου 405 χιλιάδες χιλιόμετρα. Για λόγους απλούστευσης, θεωρούμε ότι ξεκινάμε το ταξίδι μας λίγο έξω από τη Γη, ας πούμε από τον Διεθνή Διαστημικό Σταθμό (ΔΔΣ)- επομένως δε χρειάζεται να ασχοληθούμε με την εκτόξευση του πυραύλου και την περιστροφή της Γης. Υπενθυμίζουμε ότι η τροχιά του ΔΔΣ βρίσκεται σε ύψος περίπου 400 χιλιομέτρων (το ύψος αυτό αντιστοιχεί στο 0.1% περίπου της απόστασης του περίγειου), οπότε το σφάλμα στους υπολογισμούς μας θα είναι πολύ μικρό.

Ας υποθέσουμε ότι με κάποιο μαγικό τρόπο (πάλι), μπορούμε να σταματήσουμε τη σχετική κίνηση Γης και Σελήνης, καθιστώντας τα δυο σώματα ακίνητα. Φυσικά μας συμφέρει να κάνουμε κάτι τέτοιο όταν η Σελήνη βρίσκεται στο περίγειο. Θεωρώντας τότε μια μέση ταχύτητα σχετικά αργού βαδίσματος 4 χιλιομέτρων την ώρα και διαιρώντας την απόσταση του περίγειου με αυτή, βρίσκουμε ότι απαιτούνται τουλάχιστον 90 χιλιάδες ώρες για να φτάσουμε (δηλαδή περίπου 3800 ημέρες ή 10.35 χρόνια!). Φυσικά αυτά τα νούμερα αντιστοιχούν σε συνεχή κίνηση (ξεχάστε λοιπόν τα διαλείμματα για ξεκούραση!) και θα είναι διαφορετικά αν η μέση ταχύτητα είναι λίγο μικρότερη ή μεγαλύτερη. 

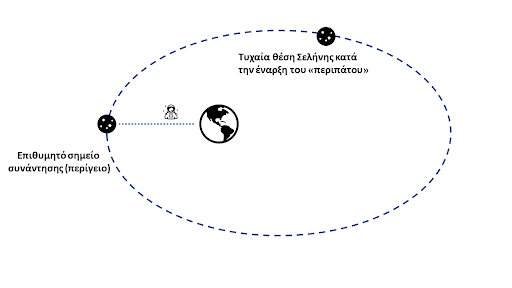
Αν ενδιαφέρεστε για παραπάνω πληροφορίες, μη σταματήσετε εδώ! Επιστρέφουμε στην πραγματικότητα, όπου η Σελήνη κινείται γύρω από τη Γη. Επομένως, όταν ξεκινήσουμε το ταξίδι μας, δε θα “περπατήσουμε” απευθείας προς τη Σελήνη καθώς όταν φτάσουμε εκεί, η Σελήνη θα έχει μετακινηθεί. Αντ’ αυτού, θα κινηθούμε προς το σημείο της τροχιάς της στο οποίο θα τη συναντήσουμε μετά από κάποιο ορισμένο χρονικό διάστημα² (Εικόνα 2). Φυσικά μας συμφέρει το σημείο αυτό να είναι και πάλι το περίγειο. Τελικά λοιπόν θα ξεκινήσουμε τον περίπατό μας προς το περίγειο, όπου αυτό βρίσκεται 10.35 χρόνια μετά³ !

Η ερώτηση αυτή μας δίνει την ευκαιρία να αναλογιστούμε ξανά τις τεράστιες αποστάσεις που συναντάμε στο ηλιακό μας σύστημα! Η απόσταση Γης-Σελήνης ισοδυναμεί περίπου με 60 φορές την ακτίνα της Γης. Αν το νούμερο αυτό σας φαίνεται μεγάλο, σας θυμίζουμε ότι αντιστοιχεί σε “μόλις” 1.28 δευτερόλεπτα φωτός. Όταν λοιπόν φτάσετε στη Σελήνη και στείλετε ένα προσυμφωνημένο φωτεινό σήμα, αυτό θα φτάσει στη Γη μετά από 1.28 δευτερόλεπτα. Αν θέλατε να “περπατήσετε” προς έναν άλλον πλανήτη, ας πούμε τον Άρη, τα πράγματα δυσκολεύουν. Ακόμα και στη μικρότερη απόσταση μεταξύ Γης-Άρη, θα χρειαστείτε περίπου 1600 χρόνια ενώ το φωτεινό σας σήμα θα χρειαζόταν λίγο παραπάνω από 3 λεπτά για να φτάσει στη Γη!

¹ Τα πραγματικά νούμερα είναι λίγο μεγαλύτερα, ωστόσο τα αποτελέσματά μας δεν αλλάζουν σημαντικά.

² Αυτή η απλή ιδέα είναι εξαιρετικά σημαντική για κάθε δορυφόρο που εκτοξεύουμε και θέλουμε να τεθεί σε τροχιά γύρω από ένα άλλο ουράνιο σώμα!

³ Φυσικά, όπως και σε άλλες περιπτώσεις στο Ηλιακό μας Σύστημα, η τροχιά της Σελήνης γύρω από τη Γη δεν είναι σταθερή, αλλά μεταβάλλεται με το χρόνο. 

⁴ Αυτό συμβαίνει διότι σε διάστημα ενός έτους, η Σελήνη ολοκληρώνει περίπου 12.4 τροχιές γύρω από τη Γη, όπως τις αντιλαμβανόμαστε από τον πλανήτη μας.

Επιπλέον υλικό (με ρεαλιστικά παραδείγματα):

1. Δείτε εδώ την τροχιά που ακολουθεί ένα διαστημόπλοιο για να φτάσει στη Σελήνη! https://en.wikipedia.org/wiki/Trans-lunar_injection
2. Διάφορες τροχιές της αποστολής Artemis: https://www.esa.int/Science_Exploration/Human_and_Robotic_Exploration/Orion/Artemis_I