Γιατί χρησιμοποιούμε «παράξενες» μονάδες στην (Αστρο)φυσική;
- Συγγραφέας: Δημήτρης Μήλλας
- 16-01-2022
- Τροποποίηση: 30-09-2023
- Δυσκολία: Εύκολο
- Κατηγορίες: Διάφορα
Στην καθημερινή μας ζωή χρησιμοποιούμε διάφορες μονάδες μέτρησης για να περιγράψουμε όσα βλέπουμε γύρω μας. Φυσικά μεγέθη όπως η ταχύτητα, ο χρόνος, η απόσταση, το βάρος (ως ανάλογο της μάζας) και πολλά άλλα χρειάζονται κάποιες μονάδες μέτρησης για να περιγράφουν σωστά. Πολλές φορές μάλιστα, ασυναίσθητα, επιλέγουμε διαφορετικές μονάδες για το ίδιο φυσικό μέγεθος.
Ας πάρουμε για παράδειγμα τη μέτρηση του χρόνου. Η διάρκεια ενός ταξιδιού σε μια εκδρομή με το αυτοκίνητο, απαιτεί συνήθως ώρες. Ένα μονοθέσιο της Formula 1 χρειάζεται λίγο παραπάνω από ένα λεπτό για την ολοκλήρωση ενός γύρου. Ο χρόνος που απαιτείται για μια περιφορά του Πλούτωνα γύρω από τον Ήλιο είναι περίπου 248 χρόνια.
Για τη μέτρηση αποστάσεων, τα πράγματα γίνονται λίγο πιο πολύπλοκα. Εκτός από το μέτρο και τα παράγωγά του, πολλές χώρες χρησιμοποιούν ίντσες, γιάρδες και μίλια ή ακόμη και πόδια! Σίγουρα θα έχετε ακούσει όμως και τις εκφράσεις «αστρονομική μονάδα» και «έτος φωτός» – το οποίο παρά το όνομά του, είναι μονάδα μήκους! Αν και η επιλογή τέτοιων «ασυνήθιστων» μονάδων θα μπορούσε να αποτελεί μια ιδιοτροπία των επιστημόνων, η χρήση τους είναι επιβεβλημένη στην έρευνα. Ας δούμε το γιατί.
Το Διεθνές Σύστημα Μονάδων, γνωστό ως SI (Système International), καθορίζει τις μονάδες μέτρησης των θεμελιωδών φυσικών μεγεθών. Ωστόσο, δε σημαίνει ότι αυτές είναι πάντοτε βολικές ή κατάλληλες για όλες τις περιπτώσεις. Ας ξαναδούμε ορισμένα από τα παραπάνω παραδείγματα χρησιμοποιώντας το δευτερόλεπτο ως μονάδα μέτρησης χρόνου, όπως προβλέπει το SI. Ένα ταξίδι 2 ωρών λοιπόν, μεταφράζεται σε 7200 δευτερόλεπτα. Πόσο σημαντική είναι τότε μια καθυστέρηση 300 δευτερολέπτων; Και αν για τη χρονομέτρηση ενός γύρου σε αγώνα Formula 1, τα 1,25 λεπτά και τα 75 δευτερόλεπτα είναι το ίδιο βολικά, τι θα λέγατε για τα 7.820.928.000 δευτερόλεπτα που απαιτούνται για μια πλήρη περιφορά του Πλούτωνα γύρω από τον Ήλιο;
Η σύγκριση αποστάσεων γίνεται ακόμα δυσκολότερη καθώς τα μεγέθη που συναντάμε ακόμα και εντός του ηλιακού μας συστήματος είναι ασύλληπτα μεγαλύτερα από αυτά με τα οποία είμαστε εξοικειωμένοι στη Γη. Η εισαγωγή υποδιαιρέσεων και πολλαπλάσιων στις μονάδες μέτρησης δεν είναι πάντα αρκετή για να λύσει το πρόβλημα.
Προσπαθούμε επομένως να τα εκφράζουμε μέσω μιας «τυπικής» κλίμακας, κατάλληλης για το εκάστοτε σύστημα. Για αποστάσεις εντός του ηλιακού μας συστήματος, τέτοια τυπική κλίμακα είναι η «αστρονομική μονάδα» (astronomical unit ή AU), η οποία ορίζεται ως η μέση απόσταση Γης-Ηλίου, δηλαδή 149.597.870,7 χιλιόμετρα (εικόνα 1). Δείτε στον παρακάτω πίνακα δυο αποστάσεις εκφρασμένες με μέτρα και αστρονομικές μονάδες.
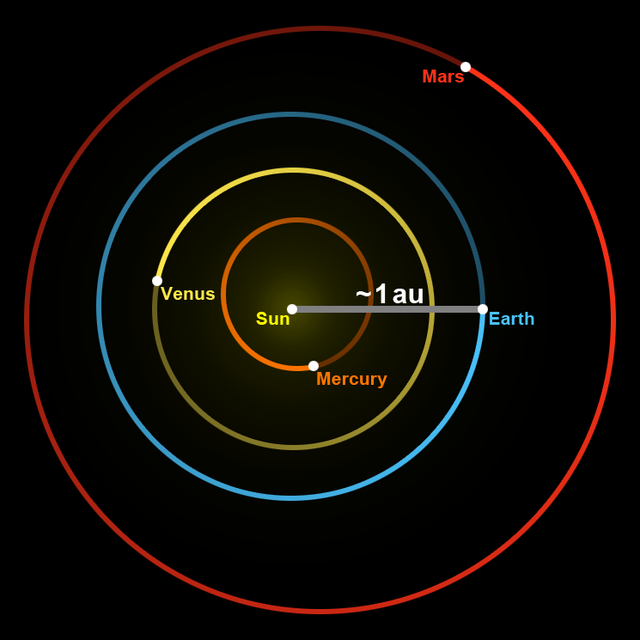
Image Credit: https://commons.wikimedia.org/wiki/File:Astronomical_unit.png
Στην πρώτη περίπτωση μπορούμε να καταλάβουμε μόνο ότι ο Πλούτωνας βρίσκεται πιο μακριά από τον Άρη. Με τη χρήση αστρονομικών μονάδων, τα νούμερα γίνονται πιο εύχρηστα και πιο άμεσα κατανοητά. Μαθαίνουμε όχι πόσο μεγάλη είναι μια απόσταση αλλά έχουμε και ένα άμεσο μέτρο σύγκρισης. Ο Άρης λοιπόν είναι σχετικά κοντά στον Ήλιο (50% πιο μακριά από τη Γη), αλλά ο Πλούτωνας είναι 40 φορές περίπου πιο μακριά!

Αν θελήσουμε να εκφράσουμε μεγαλύτερες αποστάσεις, για παράδειγμα εντός του Γαλαξία μας, ακόμα και η αστρονομική μονάδα δεν είναι επαρκής. Το κοντινότερο στον Ήλιο άστρο, ο Εγγύτατος του Κενταύρου (Proxima Centauri) βρίσκεται σε απόσταση πάνω από 290.000 αστρονομικές μονάδες – τα νούμερα γίνονται πάλι δύσχρηστα. Το πρόβλημα λύνει το «έτος φωτός», το οποίο ορίζεται ως η απόσταση που διανύει το φως σε ένα μέσο γήινο έτος (365,25 ημέρες) και ισούται με 9.460.730.472.580.800 μέτρα1.
Επίσης, η φράση “με ταχύτητα φωτός” αξιοποιείται στο έπακρο στην αστροφυσική, καθώς αποτελεί τη μέγιστη δυνατή τιμή ταχύτητας. Σε αρκετές περιπτώσεις λοιπόν, όπως για παράδειγμα σε πίδακες από ενεργούς γαλαξίες, μετράμε τις ταχύτητες που εμφανίζονται στη μελέτη μας σε μονάδες ταχύτητας φωτός.
Ανάλογες απλοποιήσεις είναι απαραίτητες και σε άλλα φυσικά μεγέθη, όπως η μάζα. Προσπαθήστε να συγκρίνετε τη μάζα του αέριου γίγαντα πλανήτη Δία, περίπου 2×1027 κιλά (δηλαδή ο αριθμός 2 ακολουθούμενος από 27 μηδενικά!) και του μεγαλύτερου από τα τρία αστέρια που σχηματίζουν το σύστημα του Πολικού Αστέρα3 (α UΜi): περίπου 11×1030 κιλά (11 με 30 μηδενικά!). Φυσικά, και οι δύο έχουν τεράστια μάζα. Αν ορίσουμε όμως την Ηλιακή μάζα ως τυπική μονάδα μέτρησης μάζας για αυτές τις κλίμακες, τότε ο Δίας έχει μόλις το ένα χιλιοστό της μάζας του Ηλίου ενώ ο α UΜi έχει μάζα πάνω από 5 φορές μεγαλύτερη2.
Τέλος, για λόγους πληρότητας, είναι σημαντικό να αναφέρουμε ότι δε δημιουργούν μόνο οι μεγάλες τιμές μεγεθών σύγχυση. Σε άλλους κλάδους της φυσικής, όπου εμπλέκονται πολύ μικροί αριθμοί, είναι βολικό να γίνονται ανάλογες τροποποιήσεις. Για παράδειγμα, τα μεγέθη των ατόμων δίνονται συνήθως σε Ångström, που ισούται με το ένα δεκάκις δισεκατομμυριοστό του μέτρου! Περισσότερα όμως, στο δεύτερο μέρος του άρθρου!
1 Ο αριθμός αυτός προκύπτει αν πολλαπλασιάσουμε την ταχύτητα του φωτός, σε μέτρα ανά δευτερόλεπτο με τον αριθμό των δευτερολέπτων από τα οποία αποτελείται ένα έτος.
2 Πέραν από τον εύκολο χειρισμό των μεγεθών, στην περίπτωση αυτή λαμβάνουμε επιπλέον πληροφορία, καθώς η μάζα παίζει ρόλο τόσο στη δημιουργία όσο και στην εξέλιξη των άστρων. Βλέπουμε ότι ο Δίας δε θα μπορούσε ποτέ να είναι αστέρας λόγω της “μικρής” του μάζας (σε σχέση με του Ήλιου) ενώ ο α UΜi είναι ένας υπεργίγαντας αστέρας!
3 https://hubblesite.org/contents/news-releases/2006/news-2006-02.html