Μπορεί μια Πεταλούδα να Επηρεάσει τον Καιρό
- Συγγραφέας: Ανδρέας Σοφιανός
- 17-10-2022
- Τροποποίηση: 30-09-2023
- Δυσκολία: Εύκολο
- Κατηγορίες: Διάφορα
Μπορεί το πέταγμα μιας πεταλούδας στην Κίνα να προκαλέσει μια καταιγίδα στη Νέα Υόρκη; Το προηγούμενο ερώτημα, πολλοί, αν όχι όλοι σίγουρα θα το έχουν ακούσει κάποτε, κάπου, τυχαία ή συμμετέχοντας σε κάποια συζήτηση… Τι ισχύει όμως στην πραγματικότητα; Πόσο επηρεάζεται ο καιρός από την επίδραση διαφόρων, μικρών και μεγάλων αλλαγών; Τι είναι το “Φαινόμενο της Πεταλούδας”;
Τα προηγούμενα ερωτήματα σχετίζονται με την εμφάνιση και την ανάπτυξη της Θεωρίας του Χάους. Η πιο διάσημη πεταλούδα στην ιστορία των μαθηματικών ανακαλύφθηκε μάλλον κατά τύχη όταν στις αρχές της δεκαετίας του 1960 ο E.D.Lorenz πειραματιζόταν με διάφορα απλοποιημένα μοντέλα για τη μελέτη του καιρού στη γήινη ατμόσφαιρα. Ένα πρωί χωρίς να γνωρίζει αυτό που θα ακολουθούσε, και αφού στρογγυλοποίησε κατά ένα χιλιοστό τις αρχικές συνθήκες1 που είχε δώσει στον Royal McBee την προηγούμενη μέρα (από 0.506127 σε 0.506!!), θα φύγει για τον καθιερωμένο του καφέ στο κυλικείο του ΜΙΤ. Όπως συχνά συμβαίνει στην επιστήμη το Αναγκαίο εκφράζεται μέσω ενός Τυχαίου γεγονότος, έτσι και εδώ το αποτέλεσμα ήταν κάτι το αναπάντεχο. Η εικόνα που πήρε ήταν τελείως διαφορετική από αυτή της προηγούμενης μέρας. Οι τροχιές αποκλίνανε αισθητά η μία από την άλλη πολύ γρήγορα.
Μέσα από τη μελέτη αυτής της πρωτόγνωρης συμπεριφοράς ο Lorenz κατέληξε σε δύο βασικά συμπεράσματα θεμελιώδους σημασίας. Το πρώτο αφορούσε τη σχέση των αρχικών συνθηκών που δίνουμε σε ένα σύστημα με το αποτέλεσμα της συμπεριφοράς που αναμένουμε. Το συμπέρασμα ήταν ότι πολύ μικρές αλλαγές στις αρχικές συνθήκες μπορούν να οδηγήσουν σε μεγάλες αλλαγές στη συμπεριφορά του συστήματος. Το δεύτερο συμπέρασμα αφορούσε την ανάδυση μιας νέας μορφής τάξης: Ο Lorenz παρατήρησε ότι το σύνολο των τροχιών του συστήματος του συγκεντρώνεται σε μία περιοχή του χώρου που πήρε την ονομασία παράξενος ή χαοτικός ελκυστής. Ο ελκυστής του Lorenz, που φαίνεται στην Εικόνα 2, δείχνει την περιοχή γύρω από την οποία συγκεντρώνονται οι τροχιές. Η περιοχή αυτή έχει καθορισμένη δομή, πράγμα που αναδεικνύει και την έννοια της “νέας μορφής τάξης” που αναφέραμε.
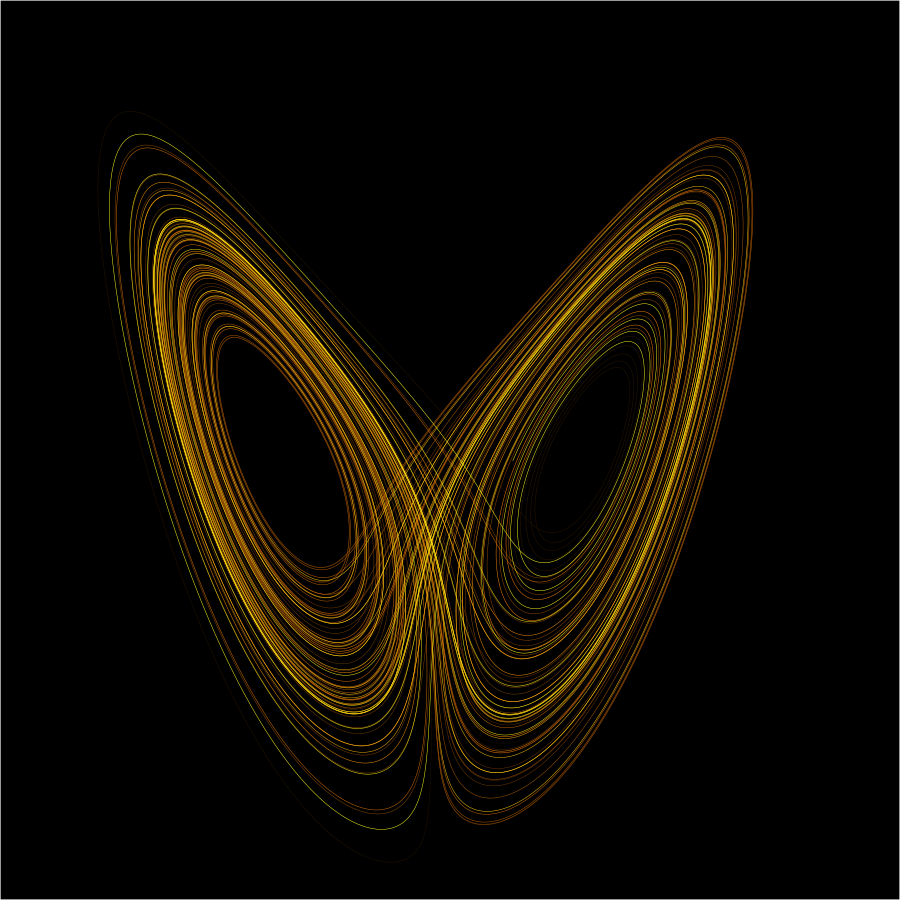
Στο προηγούμενο σχήμα αποτυπώνεται η πολυπλοκότητα αυτής της χαοτικής συμπεριφοράς, αλλά και η ομοιότητα που παρουσιάζει το σχήμα με μία πεταλούδα. Αυτή η ομοιότητα οδήγησε στη διαμόρφωση της κοινωνικής συνείδησης που σε πολλές περιπτώσεις εκφράστηκε και εκφράζεται με την άποψη ότι “μια πεταλούδα επηρεάζει τον καιρό”. Αποδεικνύεται έτσι η βαθιά επίδραση που έχει η επιστήμη σε όλες τις πλευρές της κοινωνικής ζωής.
Η απαρχές στη διαμόρφωση της Θεωρίας του Χάους βρίσκονται στις αρχές του 20ού αιώνα και την απόδειξη από τον H. Poincare της μη επιλυσιμότητας του προβλήματος των τριών σωμάτων3. Η ανάπτυξη της Θεωρίας του Χάους όπως ονομάστηκε, ήταν ραγδαία στις δεκαετίες του 1970 και 1980 και συνδέθηκε με τη μελέτη ή την ανακάλυψη πλήθους φαινομένων από το σύνολο των διαφόρων επιστημών. Τέτοια παραδείγματα μπορεί να δει κανείς από την πληθυσμιακή βιολογία μέχρι οικονομικά μοντέλα ή και την προσπάθεια ερμηνείας πρόβλεψης γεωπολικτικών συγκρούσεων και ανακατατάξεων. Η επιδραστικότητα της νέας Θεωρίας ήταν τέτοια με αποτέλεσμα πολλοί να τη θεωρούν ως την τρίτη επιστημονική επανάσταση στον 20ό αιώνα, μετά τη Θεωρία της Σχετικότητας και την Κβαντομηχανική. Η Θεωρία του Χάους συνεχίζει να επιδρά και να ανοίγει νέους δρόμους στη σημερινή έρευνα. Η ραγδαία ανάπτυξη των υπολογιστικών ικανοτήτων, μας έχει δώσει τη δυνατότητα προσομοίωσης πολύπλοκων φαινομένων που αδυνατούσαμε να μελετήσουμε στο παρελθόν. Η συμπεριφορά τεράστιων πληθυσμών, η λειτουργία των μέσων κοινωνικής δικτύωσης, η μελέτη του κλίματος είναι μερικά μόνο από τα φαινόμενα που μελετά η αναδυόμενη Επιστήμη της Πολυπλοκότητας.
Στην πορεία ανάπτυξης της επιστήμης του Χάους καμία εργασία δεν αποτέλεσε τέτοια τομή όσο η εργασία του E.Lorenz με τίτλο, “Deterministic NonPeriodic Flow” που δημοσιεύτηκε στο “Journal of the Atmospheric Sciences”. Οι έννοιες του Τυχαίου, της Μη Προβλεψιμότητας, αλλά και ο επαναπροσδιορισμός της έννοιας του Ντετερμινισμού ήρθαν ξανά στο προσκήνιο, σε πλήθος επιστημονικών πεδίων από τη Φυσική και την Τοπολογία μέχρι τη Φιλοσοφία της Επιστήμης και την Επιστημολογία.
Το μέλλον θα είναι σίγουρα το ίδιο συναρπαστικό στα πεδία του Χάους και της Πολυπλοκότητας. Ο σπουδαίος Richard Feynman σημείωνε “Τι κάνει τη φύση να συμπεριφέρεται έτσι; Πιστεύω πως οφείλεται στο ότι η φύση είναι απλή και γι’ αυτό πολύ όμορφη!”. Η Θεωρία του Χάους ανέδειξε μία νέα μορφή απλότητας που αναδεικνύεται μέσα από την πολυπλοκότητα των φαινομένων. Μία πολυπλοκότητα που συμβάλει στην καλύτερη κατανόηση του κόσμου μας.
1. Αρχικές Συνθήκες είναι οι πρωταρχικές τιμές που δίνουμε σε ένα σύστημα διαφορικών εξισώσεων (στην προκειμένη περίπτωση). Εξασφαλίζουν μια σειρά από μαθηματικές ιδιότητες των λύσεων καθώς και την αρχική κατάσταση του συστήματος. Οι αρχικές συνθήκες είναι απαραίτητη προϋπόθεση για την υπολογιστική προσομοίωση του συστήματος και στην περίπτωση των χρονοανεξάρτητων εξισώσεων του Μοντέλου Lorenz αφορούν τις αρχικές τιμές που δίνουμε στις συντεταγμένες x,y,z για το χρονικό διάστημα της προσομοίωσης. Οι αρχικές συνθήκες μαζί με τις τιμές των παραμέτρων μας δίνουν το αποτέλεσμα της Εικόνας 2.
2. Ο χώρος που αναπαριστά τις ορμές ή τις ταχύτητες του συστήματος ως προς τις αντίστοιχες θέσεις του.
3. Ο Poincare ήταν ο πρώτος που εφάρμοσε μία περισσότερο ποιοτική παρά ποσοτική προσέγγιση των προβλημάτων διαφορικών εξισώσεων και στάθηκε ιδιαίτερα στη γεωμετρική ανάλυσή τους και την πληροφορία που μπορεί να δώσει για το σύστημα. Ένα παράδειγμα προβλήματος τριών σωμάτων θα μπορούσε να είναι το Σύστημα Ήλιος-Γη-Σελήνη. Το ζητούμενο ήταν αν μπορεί να αποτελέσει ένα ολοκληρώσιμο σύστημα. Αν δηλαδή μπορεί να βρεθεί μία ακριβής λύση του συστήματος. Στο τέλος του 19ου αιώνα οι Poincare και Bruns έδειξαν ότι αυτό είναι αδύνατο.
Παραπομπές
E.D.Lorenz, “Deterministic NonPeriodic Flow”, Journal of the Atmospheric Sciences, 20(2): 130-141, 1963
J.Gleick, “Χάος, Μία Νέα Επιστήμη”, εκδ. Κάτοπτρο
Τ.Μπούντης, “Τύχη ή Βεβαιότητα, Η Διαλεκτική της Θεωρίας του Χάους”
I.Prigogine και I.Stengers, “Τάξη Μέσα στο Χάος”, εκδ. Κέδρος


