Τι είναι τα διαγράμματα Feynman;

Η σύγχρονη κατανόηση της ανθρωπότητας για τη φύση των μορίων, των ατόμων, των ατομικών πυρήνων και των στοιχειωδών σωματιδίων βασίζεται στην κβαντική μηχανική. Ειδικότερα για τον τελευταίο κλάδο, αυτό των στοιχειωδών σωματιδίων, οι μεγαλύτερες επιστημονικές ανακαλύψεις έχουν προκύψει από πειράματα που έχουν λάβει χώρα στους λεγόμενους επιταχυντές σωματιδίων. Πρόκειται για επιστημονικές διατάξεις που έχουν τη δυνατότητα να επιταχύνουν μία ή παραπάνω δέσμες σωματιδίων και είτε να τις κατευθύνουν σε ένα σταθερό στόχο είτε να τις αναγκάσουν να συγκλίνουν σε συγκεκριμένα σημεία όπου δύο δέσμες μπορούν να συγκρουστούν. Από τη σύγκρουση των σωματιδίων της δέσμης με αυτά του σταθερού στόχου ή των σωματιδίων των δύο δεσμών, μπορούν να παραχθούν νέα σωματίδια. 

Όταν οι ταχύτητες των σωματιδίων της δέσμης επιταχύνονται κοντά σε αυτή της ταχύτητας του φωτός, είναι υποχρεωμένος κανείς να αναρωτηθεί πώς μεταβάλλονται οι νόμοι της κβαντικής μηχανικής όταν συνδυαστούν με αυτούς της ειδικής θεωρίας της σχετικότητας. Το πάντρεμα αυτών των δύο θεωριών οδηγεί στη διαμόρφωση της κβαντικής θεωρίας πεδίου, ενός μαθηματικού πλαισίου που μας επιτρέπει να μελετήσουμε και να κατανοήσουμε τι συμβαίνει κατά τη σύγκρουση, ή τη σκέδαση – όπως συνήθως αναφέρεται στη σχετική βιβλιογραφία – μεταξύ στοιχειωδών σωματιδίων και να προβλέψουμε το αποτέλεσμα αυτών των σκεδάσεων, π.χ. τι είδους σωματίδια θα παραχθούν. 

Η τελευταία μεγάλη ανακάλυψη στο χώρο των στοιχειωδών σωματιδίων ανακοινώθηκε το 2012, όταν δύο ξεχωριστές ομάδες επιστημόνων από τα πειράματα ATLAS και CMS που μελετούν τις σκεδάσεις σωματιδίων που λαμβάνουν χώρα στον Μεγάλο Επιταχυντή Αδρονίων (LHC) στο CERN, ανακοίνωσαν την ανακάλυψη του μποζονίου Higgs [1]. Αυτή η ανακάλυψη επιβεβαίωσε θεωρητικές προβλέψεις για την ύπαρξη του μποζονίου Higgs που είχαν γίνει στα πλαίσια του Καθιερωμένου Προτύπου [2], της κβαντικής θεωρίας πεδίου που περιγράφει όλες τις γνωστές δυνάμεις της φύσης πλην της βαρύτητας. Η ανακάλυψη αυτή θεωρήθηκε αντάξια του βραβείου Νόμπελ Φυσικής το 2013, το οποίο απονεμήθηκε στους Francois Englert και Peter Higgs, δύο από τους θεωρητικούς φυσικούς που είχαν προβλέψει την ύπαρξη αυτού του στοιχειώδους σωματιδίου.

Πώς μπορούμε όμως να προβλέψουμε το αποτέλεσμα των σωματιδιακών σκεδάσεων; Παρόλο που εν γένει η απάντηση στην παραπάνω ερώτηση είναι μια μακρά λίστα μαθηματικών μεθόδων, το κυριότερο εργαλείο των φυσικών στην προκειμένη περίπτωση είναι τα λεγόμενα διαγράμματα Feynman. Τα διαγράμματα αυτά εισήχθησαν στην ερευνητική βιβλιογραφία από τον Richard Feynman (βραβείο Νόμπελ Φυσικής 1965) με σκοπό να απλοποιήσουν συγκεκριμένους μαθηματικούς υπολογισμούς.

Ας σχεδιάσουμε μερικά διαγράμματα λοιπόν! Αυτό που χρειάζεται κανείς είναι να ακολουθήσει τους παρακάτω κανόνες:

1.     Μπορούμε να σχεδιάσουμε δύο ειδών γραμμές, είτε ευθύγραμμα τμήματα με βέλος είτε κυματοειδείς (Εικόνα 1).

2.    Μπορούμε να συνδέσουμε αυτές τις γραμμές μόνο όταν έχουμε δύο ίσιες γραμμές με βέλη να συναντούν μια κυματιστή γραμμή (Εικόνα 2). Η κατεύθυνση των βελών είναι σημαντική! Μπορούμε να έχουμε μόνο μία γραμμή με βέλος που πηγαίνει προς τον κόμβο και μία με βέλος που βγαίνει από τον κόμβο.

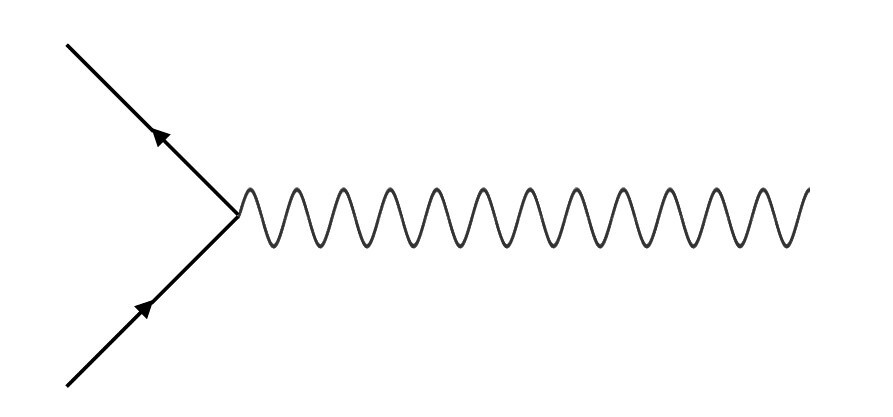
3.    Το διάγραμμα επιτρέπεται να περιέχει μόνο συνδεδεμένες γραμμές (Εικόνα 3).

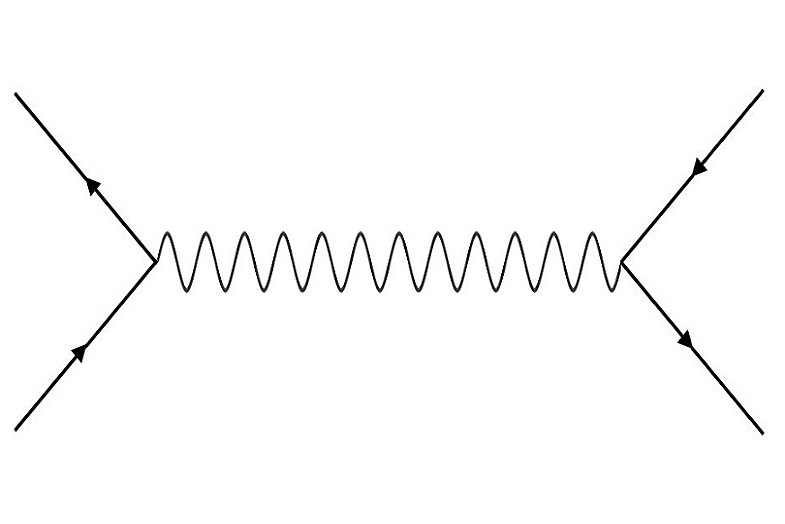
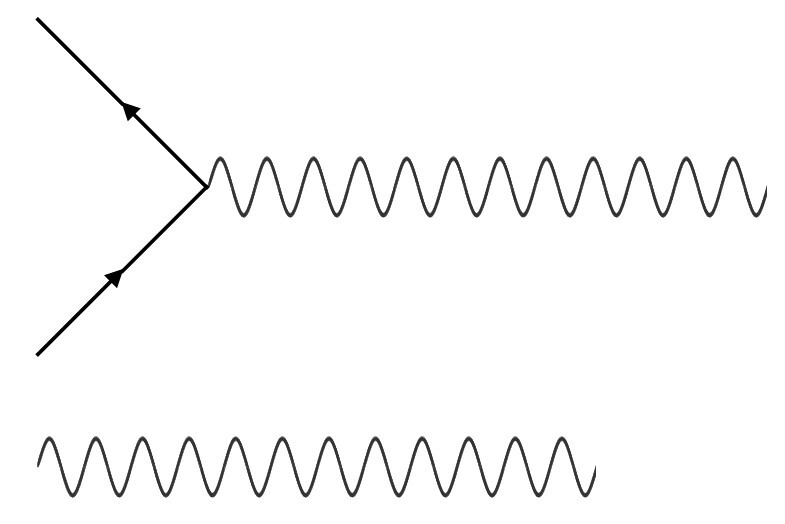
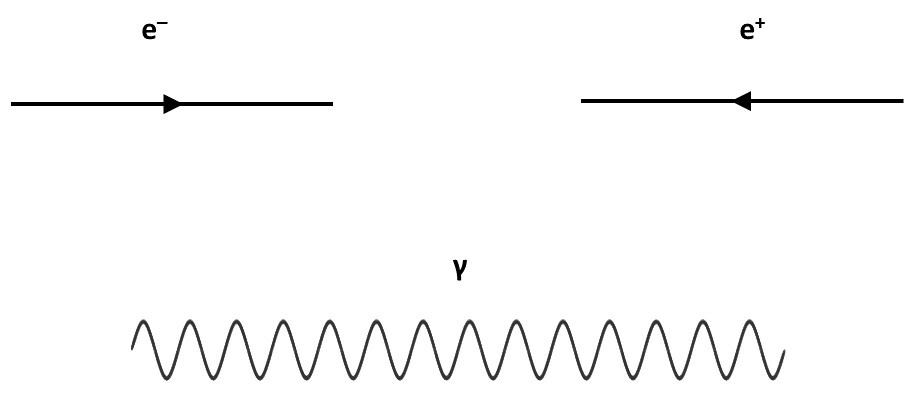
Μπορούμε πλέον να σχεδιάσουμε διαγράμματα Feynman. Πώς όμως ερμηνεύονται αυτά τα διαγράμματα; Οι γραμμές του κανόνα 1 αναπαριστούν σωματίδια. Ο κόμβος του κανόνα 2 αναπαριστά μια αλληλεπίδραση μεταξύ σωματιδίων. Έχουμε λοιπόν τα εργαλεία για να μελετήσουμε μια θεωρία σωματιδίων και τις αλληλεπιδράσεις τους. Πιο συγκεκριμένα, η θεωρία αυτή ονομάζεται Κβαντική Ηλεκτροδυναμική (Quantum Electrodynamics, QED), και περιγράφει την αλληλεπίδραση μεταξύ ηλεκτρονίων (e^–), ποζιτρονίων (e⁺) και φωτονίων (γ), τα οποία συμβολίζονται με τους παρακάτω τύπους γραμμών που συναντήσαμε στους προηγούμενους κανόνες.

Για παράδειγμα, το διάγραμμα του κανόνα 2 περιγράφει την εξαΰλωση ενός ζεύγους ηλεκτρονίου-ποζιτρονίου παράγοντας ένα φωτόνιο. Το επιτρεπτό διάγραμμα του κανόνα 3 περιγράφει αρχικά την ίδια διαδικασία, όμως στη συνέχεια το φωτόνιο παράγει ένα ζεύγος ηλεκτρονίου-ποζιτρονίου.

Τα διαγράμματα Feynman χρησιμοποιούνται για τον υπολογισμό του λεγόμενου πλάτους σκέδασης, μιας μαθηματικής ποσότητας που συνδέεται με την πιθανότητα να συμβεί μια σωματιδιακή σκέδαση στα πλαίσια της κβαντικής μηχανικής. Οι γραμμές των διαγραμμάτων δεν αναπαριστούν τις πραγματικές τροχιές των σωματιδίων στο χώρο, αλλά συνδέονται μέσω συγκεκριμένων κανόνων με μαθηματικές ποσότητες, ο συνδυασμός των οποίων δίνει τη μαθηματική έκφραση του κβαντομηχανικού πλάτους σκέδασης.

Η ικανότητά μας να πραγματοποιούμε θεωρητικούς υπολογισμούς αποτελεί αναπόσπαστο κομμάτι της ερευνητικής διαδικασίας. Τα διαγράμματα Feynman αποτελούν ένα από τα πιο σημαντικά εργαλεία στη φαρέτρα των θεωρητικών φυσικών, αφού μας δίνουν τη δυνατότητα να κάνουμε θεωρητικές προβλέψεις για φυσικά φαινόμενα που εξελίσσονται μεταξύ των θεμελιωδών συστατικών της ύλης, των στοιχειωδών σωματιδίων. Η σύγκριση των θεωρητικών προβλέψεων με πειραματικά δεδομένα που προέρχονται από σωματιδιακούς επιταχυντές, όπως ο LHC, είναι αυτή που οδηγεί στην επιβεβαίωση της κατανόησής μας για τους νόμους της φύσης, καθώς και της επέκτασης αυτής.

Επιπλέον πηγές: