Η αργοπορία Shapiro ή πώς να ελέγξετε τη γενική θεωρία της σχετικότητας με τη βοήθεια της Αφροδίτης
- Συγγραφέας: Στέφανος Τσιόπελας
- 20-06-2023
- Δυσκολία: Δύσκολο
- Κατηγορίες: Αστροφυσική
Η Γενική Θεωρία της Σχετικότητας είναι μία από τις πιο επιτυχημένες θεωρίες στη φυσική και σίγουρα μια από τις πιο διάσημες. Από τότε που διατυπώθηκε, έχει υποβληθεί σε ελέγχους όπως το περίφημο πείραμα του Eddington κατά την έκλειψη Ηλίου του 1919, έχει χρησιμοποιηθεί σε εφαρμογές, έχει εξηγήσει φαινόμενα όπως τη μετάπτωση του περιηλίου του πλανήτη Ερμή, και έχει προβλέψει άλλα που μετέπειτα παρατηρήθηκαν, με αποκορύφωμα την ανίχνευση βαρυτικών κυμάτων μερικά χρόνια πριν. Μέχρι σήμερα, χιλιάδες επιστήμονες την έχουν μελετήσει και συνεχίζουν να την μελετούν και να εργάζονται πάνω σε αυτήν με σκοπό τον έλεγχό της, την ανακάλυψη νέων προεκτάσεων της αλλά και την ενοποίησή της με τις θεωρίες που περιγράφουν τις υπόλοιπες τρεις θεμελιώδεις δυνάμεις της φύσης. Συνεχίζει επίσης να εφαρμόζεται με επιτυχία ως εργαλείο για την ανακάλυψη περισσότερων πτυχών του Σύμπαντος. Μια αρκετά εύστοχη, μη μαθηματική, σύνοψη¹ του περιεχομένου της σε μία πρόταση είναι ότι “η ύλη λέει στο χωρόχρονο πώς να καμπυλωθεί, και ο καμπυλωμένος χωροχρόνος λέει στην ύλη πώς να κινηθεί”.
Επηρεάζεται όμως μόνο η ύλη -ό,τι έχει μη μηδενική μάζα δηλαδή- από τον καμπυλωμένο χωροχρόνο;
Όπως αποδείχθηκε και στο πείραμα του Eddington, όχι: τα φωτόνια επηρεάζονται εξίσου από την καμπύλωση του χωροχρόνου. Μια παραπάνω διάσταση στην επίδραση της βαρύτητας στα φωτόνια έδωσε το 1964 ο Irwin Shapiro, προβλέποντας με βάση τις εξισώσεις της γενικής θεωρίας της σχετικότητας ότι ένας φωτεινός παλμός που διέρχεται κοντά από ένα αστρονομικό αντικείμενο θα παρουσιάσει μια χρονική καθυστέρηση στη διάδοσή του, για έναν εξωτερικό παρατηρητή, σε σχέση με το χρόνο που θα χρειαζόταν αν το αντικείμενο δεν ήταν εκεί. Η διαφορά αυτή δεν οφείλεται στο ότι ο παλμός θα διαδίδεται για κάποιο λόγο με ταχύτητα μικρότερη του φωτός, αλλά στην καμπύλωση την οποία ο χωροχρόνος θα υποστεί λόγω του βαρυτικού πεδίου του αντικειμένου. Με λίγα λόγια, το φωτόνιο αργοπορεί γιατί η χωροχρονική τροχιά του καμπυλώνεται (βλ. Εικόνα 1). Αξίζει να σημειωθεί μάλιστα ότι αυτή η κίνηση εντός του βαρυτικού πεδίου δεν θα επηρεάσει συνολικά την τελική ενέργεια που θα έχει το φωτόνιο αφότου “ξεφύγει¨ από την επίδραση του βαρυτικού πεδίου, δεν θα υποστεί δηλαδή βαρυτική ερυθρομετατόπιση ή μετατόπιση προς μικρότερα μήκη κύματος.
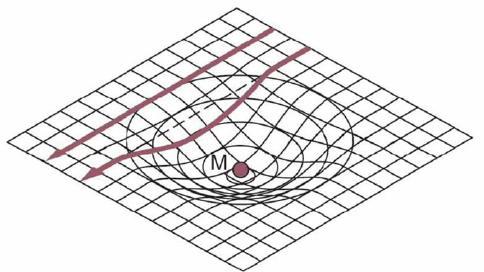
Image Credit: H. Schuch, R. Heinkelmann, Very Long Baseline Interferometry (VLBI): Accuracy limits and relativistic tests
Το πόσο θα καθυστερήσει ο φωτεινός παλμός εξαρτάται από το πόσο κοντά θα διέλθει από το αντικείμενο και φυσικά από την ίδια τη μάζα του αντικειμένου. Για την καλύτερη κατανόηση του φαινομένου αυτού, το οποίο είναι γνωστό ως αργοπορία Shapiro, και για να μπορέσουμε να ποσοτικοποιήσουμε το χρονικό διάστημα της αργοπορίας, ας φανταστούμε το εξής σενάριο (βλ. Εικόνα 2):
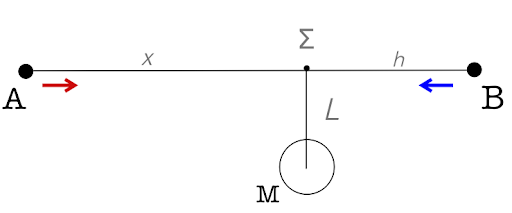
Image Credit: Στέφανος Τσιόπελας.
Έστω ότι βρισκόμαστε στο σημείο Α και χειριζόμαστε ένα ραντάρ το οποίο στέλνει ένα φωτεινό σήμα στο σημείο Β, όπου βρίσκεται ένας καθρέφτης, με σκοπό το σήμα να ανακλαστεί και να επιστρέψει πίσω σε εμάς. Ας υποθέσουμε επιπλέον ότι και τα δύο σημεία βρίσκονται κοντά σε ένα τυπικό άστρο μάζας Μ, τόσο ώστε το βαρυτικό πεδίο που “αισθάνονται” να μην είναι αμελητέο². Αυτό που θέλουμε να υπολογίσουμε είναι πόσο χρόνο θα πάρει, σύμφωνα με εμάς, στο σήμα να φτάσει στο σημείο Β και να επιστρέψει πίσω στο Α. Χάριν απλότητας, ας υποθέσουμε επιπλέον ότι εμείς, το ραντάρ και ο καθρέφτης είμαστε ακίνητοι και δε βρισκόμαστε σε τροχιά γύρω από το άστρο. Υπό αυτές τις προϋποθέσεις, και σε μια αρκετά καλή προσέγγιση, υπολογίζεται ότι ο συνολικός χρόνος θα είναι ίσος με
\[t = \frac{2(x+h)}{c}\sqrt{1-\frac{2GM}{c^2\sqrt{x^2+L^2}}} +\frac{4GM}{c^3} \ln\left(\frac{\left(x+\sqrt{x^2+L^2}\right) \left(h+\sqrt{h^2+L^2}\right)}{L^2}\right) \]όπου G η σταθερά της βαρύτητας, c η ταχύτητα του φωτός, Μ η μάζα του άστρου, ln ο φυσικός λογάριθμος και L, x, h οι αποστάσεις που σημειώνονται στο σχήμα της Εικόνας 2. Παρατηρούμε ότι στην περίπτωση που η συγκεκριμένη διαδρομή του φωτεινού σήματος πραγματοποιούνταν χωρίς την παρουσία άστρου, αν δηλαδή θεωρήσουμε ότι Μ=0, ο δεύτερος όρος στον παραπάνω τύπο μηδενίζεται, και ο όρος 2(x+h)/c καταλήγει να πολλαπλασιάζεται με τη μονάδα. Εν τέλει λοιπόν, βλέπουμε ότι σε αυτήν την περίπτωση ο παλμός θα χρειαζόταν λιγότερο χρόνο, και συγκεκριμένα ίσο με τη συνολική απόσταση που θα διέσχιζε 2(x+h) δια την ταχύτητα του φωτός c.
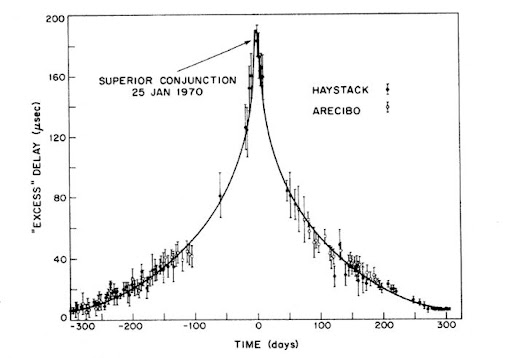
Το παραπάνω πείραμα προτάθηκε από τον ίδιο τον Ι. Shapiro το 1964 ως ακόμα ένας έλεγχος της Γενικής Θεωρίας της Σχετικότητας. Συγκεκριμένα, στα πλαίσια αυτής της πρότασης, ένα ραντάρ θα έστελνε ένα ραδιοσήμα με κατεύθυνση την Αφροδίτη, και μετά την ανάκλασή του στην επιφάνεια του πλανήτη θα επέστρεφε στη Γη, με τον Ήλιο να παίζει το ρόλο του αντικειμένου που καμπυλώνει το χωροχρόνο. Ο σκοπός του πειράματος θα ήταν, όπως είδαμε, να χρονομετρηθεί η διαδρομή του και να βρεθεί κατά πόσο η διάρκειά της θα συμφωνούσε με τη θεωρητική πρόβλεψη. Λίγα μόλις χρόνια μετά τη διατύπωση της πρόβλεψης και τον σχεδιασμό του πειράματος, ο Shapiro και οι συνεργάτες του το πραγματοποίησαν χρησιμοποιώντας τόσο την Αφροδίτη, όσο και τον Ερμή σαν “καθρέφτες” (σ.σ. σε ξεχωριστά πειράματα) με τη βοήθεια των ραντάρ των αστεροσκοπείων του Haystack και του Arecibo. Τα αποτελέσματα των μετρήσεων για την Αφροδίτη σε εύρος 600 ημερών (βλ. Εικόνα 2) και για τον Ερμή βρέθηκαν να είναι σε εκπληκτική συμφωνία με τη θεωρία, ανοίγοντας το δρόμο για τη χρήση του φαινομένου της αργοπορίας Shapiro για τον περαιτέρω έλεγχο της Γενικής Θεωρίας της Σχετικότητας σε συνθήκες ισχυρής βαρύτητας και την καλύτερη κατανόηση του σύμπαντος. Για παράδειγμα, η τεχνική αυτή της χρονομέτρησης ραδιοσημάτων έχει έκτοτε χρησιμοποιηθεί για τη μελέτη διπλών συστημάτων πάλσαρ, άλλα και τη χαρτογράφηση της κατανομής της ύλης στο σύμπαν με τη βοήθεια των ραδιοκυμάτων που εκπέμπουν οι γαλαξίες κβάζαρ (quasar).
¹Η ρήση αυτή ανήκει στον θεωρητικό φυσικό John Archibald Wheeler ο οποίος παρεμπιπτόντως καθιέρωσε και τον όρο μαύρες τρύπες και μεταξύ άλλων πρωτοστάτησε στην αναβίωση της μελέτης της γενικής θεωρίας της σχετικότητας στις δεκαετίες του ‘60 και του ‘70 στις Η.Π.Α.
²Να σημειώσουμε εδώ, ότι αυτό που έχει σημασία είναι η φωτεινή δέσμη να περνάει αρκετά κοντά από το άστρο, ώστε να “αισθάνεται” το βαρυτικό του πεδίο. Τα σημεία Α, Β δεν είναι απαραίτητο να “νιώθουν” τη βαρυτική επίδραση του άστρου, αλλά στην περίπτωση αυτή αλλάζει λίγο η εξίσωση, χωρίς βέβαια να αλλάζει ο χαρακτήρας του φαινομένου: η παρατηρούμενη αργοπορία!


