Κβαντική πλασμονική: εισάγοντας κβαντικές διορθώσεις σε ένα κλασικό πρόβλημα
- Συγγραφέας: Χρήστος Τσερκέζης
- 22-04-2022
- Τροποποίηση: 24-09-2023
- Δυσκολία: Δύσκολο
- Κατηγορίες: Φυσική
Σε προηγούμενο άρθρο είδαμε πώς η οπτική διέγερση συλλογικών ταλαντώσεων των ελεύθερων ηλεκτρονίων ενός μετάλλου (πλασμόνια) βρίσκει σημαντικές τεχνολογικές εφαρμογές, συμπεριλαμβανομένης της υπερνίκησης του ορίου της περίθλασης και του σχεδιασμού οπτικών αισθητήρων. Ένας από τους σημαντικότερους παράγοντες που οδήγησαν στην τόσο γρήγορη άνθηση της πλασμονικής στα τελευταία είκοσι χρόνια ήταν η δυνατότητα θεωρητικής αντιμετώπισης του προβλήματος μέσω της επίλυσης των εξισώσεων του Maxwell –αναλυτικά ή αριθμητικά—χρησιμοποιώντας για την περιγραφή του μετάλλου την απλή διηλεκτρική συνάρτηση που προβλέπει το μοντέλο ελεύθερων ηλεκτρονίων του Drude, ή πειραματικά δεδομένα από ελλειψομετρία λεπτών μεταλλικών πλακιδίων.
Η κατάσταση αυτή άρχισε να αλλάζει δραστικά στις αρχές της προηγούμενης δεκαετίας, οδηγούμενη και πάλι από την πρόοδο της νανοτεχνολογίας. Νανοδομές με διαστάσεις λίγων νανομέτρων, ή με μεταξύ τους αποστάσεις ακόμα και κάτω του νανομέτρου, ήταν πλέον εφικτό να παραχθούν με ακρίβεια στο εργαστήριο. Σε αυτές τις περιπτώσεις, η κλασική περιγραφή που αναφέρουμε παραπάνω προέβλεπε έναν αφύσικο απειρισμό της ενίσχυσης του ηλεκτρικού πεδίου, που βέβαια δε μετρήθηκε ποτέ πειραματικά και αντιβαίνει στη διαισθητική επιστημονική πεποίθησή ότι η φύση απεχθάνεται τους απειρισμούς. Παράλληλα, οι οπτικοί συντονισμοί στα μετρούμενα φάσματα σκέδασης ή απορρόφησης παρουσίαζαν συστηματική απόκλιση από τις θεωρητικές προβλέψεις, με το σφάλμα να μεγαλώνει όσο μικρότερο γίνεται το υπό εξέταση σωματίδιο. Έγινε λοιπόν σαφές ότι είχε έρθει η στιγμή να τροποποιηθεί η θεωρία, και να ληφθούν υπόψη στοιχεία από την κβαντομηχανική περιγραφή του μετάλλου και τη φυσική στερεάς κατάστασης, ανοίγοντας το δρόμο για το πεδίο της κβαντικής πλασμονικής. Τρία είναι τα κύρια φαινόμενα που πρέπει να λαμβάνονται υπόψη σε μελέτες δομών στο κάτω άκρο της νανοκλίμακας: η ηλεκτρονική θωράκιση, η υπερνίκηση των φραγμών δυναμικού του μετάλλου, και οι ενισχυμένες από συγκρούσεις στην επιφάνεια απώλειες απορρόφησης [1].
Η πρώτη περίπτωση, είναι η αποκαλούμενη μη τοπικότητα. Δουλεύοντας στη νανοκλίμακα, πρέπει να λαμβάνει κανείς υπόψη ότι η απόκριση του μετάλλου σε ένα συγκεκριμένο σημείο (ηλεκτρική μετατόπιση) , εξαρτάται από τη διέγερση (εφαρμοζόμενο πεδίο) στην άμεση γειτονιά του, σε εύρος που καθορίζεται από τον κυματάριθμο Fermi του μετάλλου [***]. Απαιτούνται λοιπόν μη τοπικές διηλεκτρικές συναρτήσεις που, στα πλαίσια μιας απλής υδροδυναμικής περιγραφής του ηλεκτρονικού αερίου, ήταν γνωστές ήδη από τη δεκαετία του 1930 και τη δουλειά του Felix Bloch, ενώ πιο σύνθετες μορφές που να λαμβάνουν καλύτερα υπόψη την αλληλεπίδραση ανταλλαγής και συσχέτισης έχουν προταθεί πρόσφατα. Αυτό που περιγράφουν τέτοια μοντέλα είναι ουσιαστικά η ηλεκτρονική θωράκιση (screening): το επαγόμενο φορτίο δεν εντοπίζεται αυστηρά στη διεπιφάνεια μετάλλου-περιβάλλοντος, όπως προβλέπει η κλασική θεωρία, αλλά έχει μια χωρική έκταση μέσα στο μέταλλο, και τα εσωτερικά φορτία θωρακίζουν αυτά που βρίσκονται πιο κοντά στην επιφάνεια, σαν τον σέντερ στο μπάσκετ που βγαίνει να βοηθήσει τον γκαρντ. Το αποτέλεσμα είναι το σωματίδιο να συμπεριφέρεται ως δυνητικά μικρότερος ταλαντωτής, οδηγώντας σε μια μετατόπιση των οπτικών συντονισμών του σε μικρότερα μήκη κύματος σε σχέση με την κλασική πρόβλεψη. Η συμπεριφορά αυτή παρατηρείται σε νανοσωματίδια ευγενών μετάλλων όπως ο χρυσός και ο άργυρος (τα βασικά συστατικά της παραδοσιακής πλασμονικής), όπου πράγματι τα ηλεκτρόνια της d στιβάδας θωρακίζουν τα ελεύθερα ηλεκτρόνια s [2].
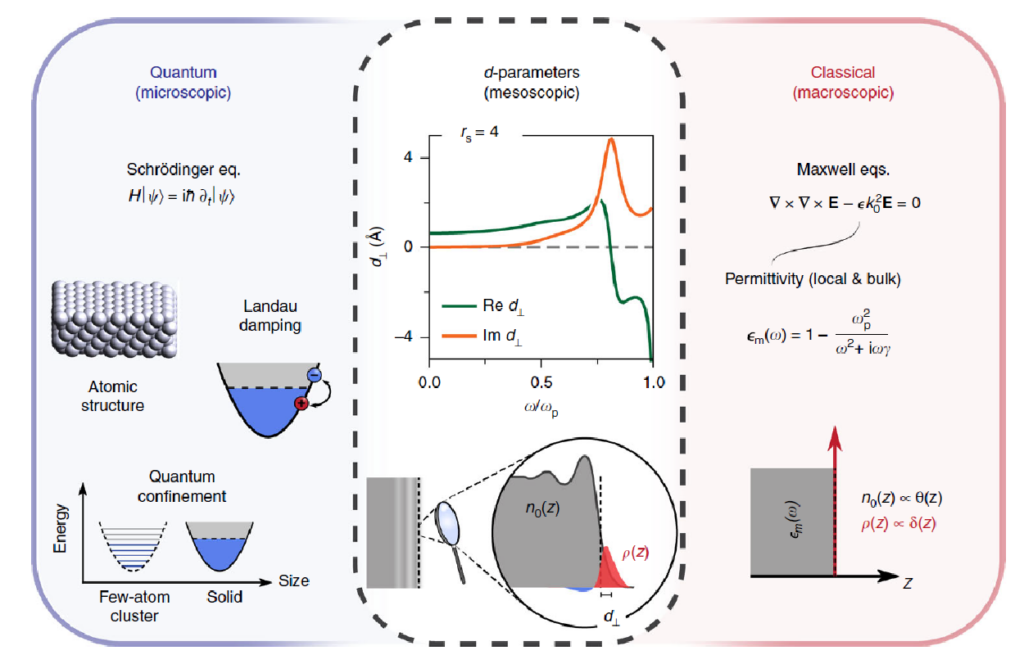
Στη μέση, η μεσοσκοπική περιοχή: οι εξισώσεις του Maxwell επιλύονται με μη τοπικές συναρτήσεις απόκρισης και κατάλληλα τροποποιημένες συνοριακές συνθήκες, ώστε να συμπεριλάβουν βασικά στοιχεία της κβαντικής συμπεριφοράς σε έναν μακροσκοπικό υπολογισμό. [Σχήμα από την αναφορά 5]. Image Credit: Χρήστος Τσερκέζης
Οι υδροδυναμικές περιγραφές γνώρισαν σχετική επιτυχία, αλλά και αρκετή κριτική, γιατί στις απλές τους εκφάνσεις περιλαμβάνουν μια κάπως χοντροειδή προσέγγιση: η συνάρτηση έργου του μετάλλου (η ενέργεια απόσπασης ενός ηλεκτρονίου) θεωρείται άπειρη, που σημαίνει ότι τα ηλεκτρόνια είναι αυστηρά περιορισμένα στο εσωτερικό του μετάλλου (συνοριακή συνθήκη «συμπαγούς τοίχου»). Όμως, κβαντομηχανικές μελέτες για σωματίδια λίγων δεκάδων/εκατοντάδων ατόμων έδειξαν ότι σε μέταλλα που ακολουθούν καλά το μοντέλο jellium (μια «σούπα» ελεύθερων ηλεκτρονίων σε ένα ομοιογενές θετικό υπόβαθρο και χωρίς άλλες σύνθετες αλληλεπιδράσεις) όπως το νάτριο, ο φραγμός δυναμικού είναι μικρός, και υπάρχει σημαντική πιθανότητα κάποια ηλεκτρόνια να τον υπερβούν (να πηδήξουν από την άλλη πλευρά του τοίχου). Αυτό οδηγεί σε δυνητικά μεγαλύτερους ταλαντωτές, και άρα μετατόπιση του συντονισμού σε μεγαλύτερα μήκη κύματος. Ακόμα πιο δραματικές είναι οι συνέπειες στην περίπτωση διμερών (δύο σωματίδια σε απόσταση λίγων δεκάτων του νανομέτρου, όπου πλέον διευκολύνεται η πιθανότητα εμφάνισης του φαινομένου σήραγγας, και τα σωματίδια συμπεριφέρονται σαν ένα ενωμένο σύστημα, παρότι αυστηρά δεν είναι σε επαφή [3].
Τέλος, είναι πειραματικά γνωστό ήδη από τη δεκαετία του 1960 ότι όσο μικραίνει το μέγεθος των σωματιδίων, τόσο περισσότερο διευρύνονται οι κορυφές συντονισμού στα φάσματα, ενδεικτικό των ισχυρών απωλειών. Διάφορες εξηγήσεις έχουν εμφανιστεί με την πάροδο των χρόνων, από την επιφανειακή τραχύτητα (άρα περισσότερες συγκρούσεις των ηλεκτρονίων) μέχρι τον κβαντικό εντοπισμό (διακριτές ενεργειακές στάθμες και απώλειες λόγω μεταβάσεων μεταξύ τους). Η επικρατούσα εξήγηση σήμερα αποδίδει τον σημαντικότερο ρόλο στην επιφανειακά ενισχυμένη απόσβεση Landau: οι συγκρούσεις των ηλεκτρονίων με τα «τοιχώματα» τους δίνει την επιπλέον ορμή που χρειάζονται για να μεταβούν σε ανώτερη ενεργειακή στάθμη στο διάγραμμα ζωνών του μετάλλου, και να δημιουργήσουν ζεύγη ηλεκτρονίων-οπών, αφαιρώντας έτσι φορείς από το πλασμόνιο. Τη συμπεριφορά αυτή μιμείται αποτελεσματικά μια γενικευμένη υδροδυναμική περιγραφή, που λαμβάνει υπόψη και τη διάχυση, εκτός από τη ροή, του ηλεκτρονικού αερίου [4].
Το κοινό χαρακτηριστικό των περισσότερων μοντέλων για την περιγραφή αυτών των φαινομένων είναι η προσπάθεια να εισαγάγουν κάποια στοιχεία της κβαντικής περιγραφής σε ειδάλλως κλασικούς υπολογισμούς. Και συνήθως καλύπτουν ικανοποιητικά μία, ή στην καλύτερη περίπτωση δύο από τις παραπάνω συμπεριφορές, αλλά όχι όλα τα φαινόμενα ταυτόχρονα. Θα ρωτήσει κανείς, και γιατί δεν κάνουμε απευθείας την κβαντική περιγραφή που θα τα πιάσει όλα; Η απάντηση είναι ότι για τα συστήματα που απασχολούν τις εφαρμογές της πλασμονικής, μεγέθους αρκετών δεκάδων νανομέτρων, πρέπει να επιλύσει κανείς ένα σύστημα με κάποια εκατομμύρια ηλεκτρόνια, και να λάβει υπόψη όλες τις μεταξύ τους αλληλεπιδράσεις, αλλά και τη μη διακρισιμότητα των ηλεκτρονίων. Για ένα σύστημα δύο ηλεκτρονίων, δεν έχουμε τη δυνατότητα να πούμε ότι το ηλεκτρόνιο α είναι στη θέση 1 και το β στη θέση 2 ή το ανάποδο (γιατί τα ηλεκτρόνια δεν έχουν ονόματα α και β), αλλά πρέπει να λάβουμε υπόψη και τους δύο γραμμικούς συνδυασμούς αυτών των πιθανοτήτων. Σε ένα σύστημα με εκατομμύρια ηλεκτρόνια, οι παράμετροι είναι τόσες που δεν μπορεί κανείς να ελπίζει να λύσει το πρόβλημα αριθμητικά (εκτός αν κάποια μέρα έχουμε όλοι στα σπίτια μας κβαντικούς υπολογιστές, κρατήστε μου δύο).
Πέρα από τις πρακτικές μικρο-λεπτομέρειες, ακόμα και μια κβαντομηχανική ατομιστική περιγραφή (όταν είναι εφικτή) έχει πρόβλημα στην περίπτωση των ευγενών μετάλλων, μια και περιλαμβάνει μεγάλη ελευθερία στην προσαρμογή των όρων ανταλλαγής-συσχέτισης (στην πράξη μια τέτοια «θεωρητική» περιγραφή βασίζεται σε προσαρμογή σε πειραματικά δεδομένα). Μια λύση, που μπορεί μάλιστα να εφαρμοστεί σε σωματίδια κάθε μεγέθους, έχει προταθεί πολύ πρόσφατα [5]. Βασίζεται στην εισαγωγή συναρτήσεων απόκρισης της επιφάνειας, τις λεγόμενες παραμέτρους Feibelman [6], οι οποίες περιγράφουν τη μέση θέση του επαγόμενου φορτίου και ρεύματος: Η ιδέα είναι ότι απαιτείται να κάνει κανείς μία μόνο φορά έναν κβαντικό υπολογισμό για την απόκριση μιας διεπιφάνειας μετάλλου-διηλεκτρικού, από τον οποίο μαθαίνει πόσο και προς ποια κατεύθυνση μετατοπίζεται το κέντρο της πυκνότητας επαγόμενων φορτίων σε σχέση με τον μαθηματικό ορισμό της επιφάνειας, και αντίστοιχα για το τυχόν επαγόμενο ρεύμα. Με τον τρόπο αυτό, η πληροφορία του αν κυριαρχεί η θωράκιση ή η υπερπήδηση του φραγμού δυναμικού εμπεριέχεται στο πραγματικό μέρος των συναρτήσεων απόκρισης, ενώ οι μηχανισμοί απόσβεσης αντιστοιχούν στο φανταστικό τους μέρος. Οι συναρτήσεις αυτές εισάγονται στη συνέχεια ως απλές τροποποιήσεις των συνοριακών συνθηκών σε οποιαδήποτε κλασική υπολογιστική μέθοδο.
Αν έχει όντως δοθεί μια οριστική απάντηση στο πρόβλημα των κβαντικών διορθώσεων στην πλασμονική θα φανεί στο μέλλον. Και μόνο η αναζήτηση της λύσης όμως, οδήγησε σε μια ιδιαίτερα γόνιμη δεκαετία για την πλασμονική, οδηγώντας στην παρατήρηση νέων φαινομένων, την πρόταση νέων εφαρμογών, και κυρίως, θέτοντας το ερευνητικό πεδίο σε πιο συμπαγή θεμέλια, βασισμένα στη φυσική συμπυκνωμένης ύλης και την κβαντική μηχανική, ανοίγοντας νέους ορίζοντες για την ερχόμενη δεκαετία.
Βιβλιογραφία
[1] P. E. Stamatopoulou and C. Tserkezis, Finite-size and quantum effects in plasmonics: manifestations and theoretical modelling, Opt. Mater. Express 12, 1869 (2022).
[2] S. Raza et al., Nonlocal optical response in metallic nanostructures, J. Phys.: Condens. Matter 27, 183204 (2015).
[3] W. Zhu et al., Quantum mechanical effects in plasmonic structures with subnanometre gaps, Nature Commun. 7, 11495 (2016).
[4] N. A. Mortensen et al., A generalized non-local optical response theory for plasmonic nanostructures, Nature Commun. 5, 3809 (2014).
[5] P. A. D. Gonçalves et al., Plasmon-emitter interactions at the nanoscale, Nature Commun. 11, 366 (2020).
[6] P. J. Feibelman, Surface electromagnetic fields, Prog. Surf. Sci. 12, 287 (1982).


